MuJoCo-XLA (MJX)環境にてロボット犬(UnitreeGo1)の歩行学習のためにPPOをFlax NNXで実装します。
- Jax/Flax NNXとは
- Massively Parallel Reinforcement Learning (大規模並列強化学習)
- 大規模並列強化学習のためのプラットフォーム
- Unitree社のロボット犬
- PPO(Proximal Policy Optimization)
- Sim2Realギャップ問題
- ロボット犬向けPPOの実装
- トレーニング結果
- 次:GRPO

Jax/Flax NNXとは
Flax NNXとはGoogle Deepmindの開発するJAXベースの深層学習ライブラリFlaxの新APIです。2020年リリースの旧API(Flax Linen)では関数型の思想で厳密に状態管理するためコードが煩雑になりがちというつらさがあったのに対して、2024年にリリースされた新API(Flax NNX)では状態管理の透過性を一定あきらめることでPytorchライクなシンプルな記法でコードを記述することが可能となりました。
シェアとしては依然PytorchとTensorflowの2強状態が続いていますが、例えばLLMのRLHF/RLVRのような高計算負荷ユースケースでは分散学習とパフォーマンスに強みを持つJAX/Flaxは有力な選択肢であるため、新APIで他フレームワークユーザーが利用しやすくなったことにより今後Flax活用の裾野が広がることが期待できます。
詳細は前記事を参照:
horomary.hatenablog.com
Massively Parallel Reinforcement Learning (大規模並列強化学習)
過去10年間の深層強化学習研究から得られた一つの経験則として、『高度な推論を必要としないタスクであれば膨大な試行回数を重ねることで、そのほとんどは強化学習で解決可能だ』ということが分かってきました。とはいっても、現実環境で無数の試行を行うことはコスト観点から多くの場合に実現困難ですが、しかし、信頼できるシミュレータが利用可能な環境であれば試行回数でのゴリ押しも実現可能な選択肢となります。
とくにロボティクス分野においては、GPU上で大規模並列実行が可能な物理エンジンを活用し、膨大な試行回数でゴリ押し強化学習を行うMassively Parallel Reinforcement Learning というアプローチが近年のトレンドの一つとなっているようです。

大規模並列強化学習のためのプラットフォーム
Massively Parallel Reinforcement Learning (大規模並列強化学習)のためのロボティクス向け物理エンジンとして、代表的にはMujoco XLA (MJX)、NVIDIA Isaac Lab、Genesis が利用可能です。本稿ではpipのみで完結するセットアップの手軽さとJAXとの相性の良さからMuJoCo XLA (MJX)を採用しますが、それぞれ異なる特長があるので目的に応じて使い分けるのがよいでしょう。
MuJoCo XLA(MJX): アルゴリズム研究者向け
MuJoCo XLA (MJX)は、連続値向け強化学習アルゴリズムの標準ベンチマークとして長く使われているMujoco物理エンジンをGoogle DeepmindがJAX(XLA)で再実装したものであり、要するにGPU/TPU上で超高速に並列実行できるよう再設計されたMuJoCoと言えます。強化学習ベンチマークとしての実績が豊富、かつpipインストールのみで完結する環境構築の容易さから、強化学習アルゴリズムの開発・検証用途として最適な選択肢でしょう。
NVIDIA Isaac Lab: ロボット開発者向け
Isaac LabはNVIDIAの提供するロボット開発のための統合プラットフォーム*1であり、PhysXエンジンによる高速・高忠実度の物理シミュレーションとフォトリアリスティックなレンダリングを強みとしています。自作ロボットを用いてシミュレータ上で獲得した動作を実世界へ転移するSim2Realワークフローの簡易化を志向していることから、ハードウェア寄りのロボット開発者に最適な選択肢でしょう。 ただし動作要件が厳しいので環境構築にハマると死ぬ*2。

Genesis: 先進的な取り組みに対応
Genesisはtaichiエンジンに支えられた圧倒的なパフォーマンスに加え、従来の剛体物理シミュレータでは扱いにくいソフトロボットや流体環境への対応、生成AIとの組み合わせなど様々な先進的な取り組みを提供するプラットフォームとなっています。Genesisでしかできないことをやりたい場合はもちろん、pytorchユーザーならセットアップが簡単っぽいのでこの種のシミュレータをとりあえず試してみたい、というような際にもお勧めできるかと思います。

Unitree社のロボット犬
本稿では、訓練対象のロボット犬としてUnitree Robotics社のGo1モデルを使用します。
以前からunitree社のロボットは低価格ながら高性能として定評がありましたが、近年は生成AIブームに乗ったことで同社は汎用ロボット市場においてますます存在感を強めています。とくにロボット犬シリーズについてはイケてるスタートアップや大企業のAÌ部門でDX感を演出する狛犬としての採用も広がっているようです。(この場合、だいたいVRヘッドセットと3Dプリンターも一緒に観測される)

Unitree社製ロボットのMujoco向けモデルは、今回使用するGo1だけでなくさらに新型のGo2やヒト型のG1などまでmujoco_menagerieから一通り利用可能です。
PPO(Proximal Policy Optimization)
※画像はJohn Schulmanの講義資料より
強化学習には様々なアルゴリズムがありますが、連続値コントロールタスクにおいてはサンプル効率重視の場合はSAC(Soft Actor Critic)、そうでない場合はPPO(Proximal Policy Optimization)が選ばれることが多いようです*3。今回は大規模並列シミュレータが利用可能につきサンプル効率を気にする必要が全くないのでPPOを採用します。
PPOはTRPOの後継手法という位置づけで提案された手法です。方策勾配定理は報酬を最大化するための方策パラメータの勾配方向を教えてくれますが、適切な更新サイズについては何も教えてくれないためしばしば学習が不安定化します。そこで、TRPOでは現在方策πθとデータ収集方策πθ_oldのKLダイバージェンスを制約項として与えることで極端なパラメータ更新を回避します*4。


TRPOは高性能であるものの、毎回の勾配更新ごとにラグランジュ乗数法で制約付き最適化問題をまじめに解くので計算量が非常に大きく、大規模ニューラルネットワークに適用することができません。この問題の解決のためにシンプル化されたTRPOとして提案された後継手法がPPOです。PPOでは方策更新が大きくなりすぎた場合にはクリップしてしまうことで暗黙的なKL制約を与えるというトリックにより、計算量を大幅に減らしつつTRPOの目的である極端なパラメータ更新防止を実現します。

なお、性能そのものについてはPPOとTRPOでほとんど差がないことが検証論文にて報告されています。論文のベンチマークスコア上ではPPOはTRPOより高い性能を示しますが、これは『実装レベルの細かいテクニック』によって得られたものであり、コアアルゴリズムに由来するものではない、とのことです。
[1709.06560] Deep Reinforcement Learning that Matters
[2006.05990] What Matters In On-Policy Reinforcement Learning? A Large-Scale Empirical Study
『実装レベルの細かいテクニック』とは、例えば「確率方策のモデル化方法」「観測のRunningStatsによる正規化」、「パラメータの初期化スキーム」などです。本稿のPPOではこのようなテクニックまで主要なものは実装していきます。
Sim2Realギャップ問題
どんなに精密な物理シミュレーターであっても現実環境とシミュレーション環境における一定の乖離は避けられず、シミュレーション環境内での強化学習で訓練したロボットをそのまま現実環境に持っていってもうまく動作しないという「Sim2Realギャップ」がしばしば問題となります。
Sim2Realギャップ問題は盛んに研究されているトピックであり、さまざまな軽減アプローチがあるのですが、本稿のPPOではドメインランダム化と非対称Actor-Criticの2つのテクニックのみ採用しました。
ドメインランダム化(Domain Randomization)
ロボットの関節動作の滑らかさや床面の摩擦係数/反発係数などは動作獲得において重要なパラメータではあるものの、そもそも個体差もあるためにシミュレーションと現実を完全に一致させることが困難です。そこで、シミュレーション環境でモデルを学習させる際にこれらのパラメータをランダムに変化させることで多様な条件下で動作する頑健性を獲得させよう、というのがドメインランダム化という手法です。これによりシミュレーションで学習した動作を現実環境へスムーズに転移させることが可能となります。
非対称Actor-Critic
非対称アクタークリティックでは、クリティック(価値関数)がアクター(方策関数)よりも多くの情報や特権的な情報(privileged information)を利用して学習します。この「特権的な情報」とは、通常アクターが現実世界で利用できない、シミュレーション環境でしか得られない情報(例:物体までの正確な距離、隠れた物体の位置など)です。特権情報の利用により、クリティックがより正確な価値評価を学習できるため、アクターの訓練を効率的にガイドできるようになります。
クリティックは方策の訓練時にしか使われないため、現実環境で追加訓練をしない場合には特権情報の利用は問題になりません。とはいえ、シミュレーション環境での動作獲得後、現実環境でも微調整のために追加学習を行いたいというのもよくある状況です。このような場合は、Teacher-Student学習により、特権情報を予測するというアプローチをとることができます。

ロボット犬向けPPOの実装
ようやく本題。Mujoco-XLA (MJX)環境にてロボット犬(UnitreeGo1)の歩行学習のためにPPOをFlax NNXで実装します。なお、本稿のPPOをbraxのPPO実装をベースとして、見通しの良さを最優先にFlax NNXで再実装したものであることにご留意ください。
実装全文:
github.com
環境構築
Installation — JAX documentation
CUDA未導入のクリーンな環境であればpipインストールで環境構築が完了します。ただし、NVIDIA GPU driverの事前インストールのみ必要です。
pip install "jax[cuda12]" flax mujoco-mjx playground
トレーニングループの実装
基本的なトレーニングループです。OpenAI Gym形式に慣れている場合はそれほど違和感のないコードになっているはずですが、state内にすべての情報(obs, reward, doneなど)が格納されていることに注意が必要です。
また、環境(env)はjax.vmapによって並列化(ベクトル化)されているため、state にはNUM_ENVS = 4096環境分のstate情報が含まれています。
環境の大規模並列化
MuJoCo XLAのラッパーライブラリであるMuJoCo Playground(mujoco_playground)を使用して環境を呼び出します。MuJoCo PlaygroundはMJXのためのgymといった感じで、環境の並列化やエピソードの自動リセットなどさまざまな便利機能を提供します。
なお、wrapperを使わない場合には、 step_fn = jax.jit(jax.vmap(env.step)) とすれば環境をベクトル化することが可能です。MJXがJAXで実装されているからこそのお手軽な並列化であり、さらにvmapをpmapに変更することで複数GPUでの並列化も簡単に実装可能です。
Squashed Gaussian方策(TanhNomal方策)
PPOの方策関数は確率分布であれば何でもよいので、最もナイーブには観測を入力として正規分布のパラメータ(μ, σ)を出力するガウス方策を使用することができます。しかしロボティクス向けの環境ではアームの角度やモーターのトルクなど、行動が有限な範囲に制限されていることがよくあります。一方で単純なガウス方策は無限の範囲を持つためそのまま使うと学習が不安定になることがあります。
このような有限範囲における連続値コントロール環境では、正規分布をTanhで押しつぶしたSquashed Gaussian方策の採用が推奨されます。

なお、SquashedGaussian方策の確率密度は確率変数の変数変換により、以下のように計算できます。

数式的にはこれでいいのですが、ただ右辺第二項が数値的に不安定(桁落ちでln0が発生しうる)なため、実装上はさらに展開して計算します。

まとめると以下のような実装になります。
なお、連続値コントロールだとactivationにもtanhを使うのがよいとされていますが、元ネタにしたbraxのPPO実装に倣いsiluを採用しました。
観測の正規化
大変地味ながら性能に与える影響が極めて大きいのがRunningStatsによる観測情報の正規化です。バッチノーマライゼーションなどと同様に、訓練中にデータの平均と分散を記録し、その情報を使って推論時にデータを正規化することで学習を安定させます。やるべきこと自体はシンプルなのですが、これをナイーブに実装すると分散の算出のために全データ保持が必要となるため、メモリへの負荷が大変なことになります。
このため RunningStatsではWelford's online algorithm (Wikipedia)というメモリ効率のよい実装を行っています。
GAE(Generalized Advantage Estimation)
アドバンテージ関数としてはGAE(Generalized Advantage Estimation)を採用します。GAEはn-step returnにもとづくアドバンテージ関数の一般化という感じで、ハイパラであるλを0に設定した場合は1ステップリターン、1に設定した場合はモンテカルロリターンに相当します。

代理目的関数の最大化(ロス関数)
これは論文通りに実装するだけなので簡単。
アドバンテージのミニバッチ内正規化とエントロピーボーナスはあってもなくてもさほど性能に影響ないらしいですがせっかくなので実装しました。
トレーニング結果
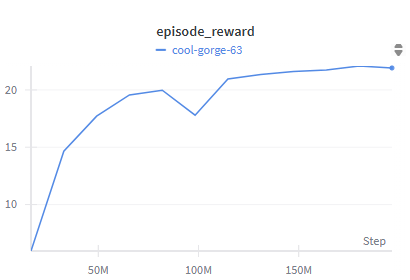
RTX4080でトータル2億(200M)環境ステップのトレーニングを実行。データ収集は秒速50万環境ステップくらいと十分に高速であるものの、方策更新がボトルネックになるので結局はトータル1時間くらいかかりました。それでも十分速いのでヨシ。
自作PPOでGo1君の走行にようやく成功。初期実装では立つのがやっとだったが、「エントロピーボーナス付きTanhNormal方策」「SiLU活性化関数」「RunningStatsによる観測の正規化」で大幅に性能が向上した。やはり連続値コントロールは難しい... pic.twitter.com/0fP06tIaP0
— めんだこ (@horromary) August 7, 2025
次:GRPO
そのうち
