CMA-ES（共分散行列適応進化戦略）の Python実装

実用性の高いブラックボックス最適化手法 CMA-ES(共分散行列適応進化戦略) のpython実装例を簡単なアルゴリズム解説とともに紹介します。

f:id:horomary:20210117213110g:plain:w400

f:id:horomary:20210117224720p:plain:w400

はじめに
アルゴリズム概要
実装の確認

はじめに

CMA-ESは連続最適化問題におけるブラックボックス最適化手法のひとつです。ブラックボックス最適化、すなわち最適化したい関数の中身がまったくわからなくてもOKなので極論どんな問題にでも適用可能で、確率的な探索を行うアルゴリズムであることから観測ノイズに強い上に、調整の難しいハイパーパラメータが存在しないので現実の問題に適用しやすい優秀な手法です。

本記事ではCMA-ESの考案者であるHansen氏らが2016年に執筆したCMA-ESのチュートリアル論文（[1604.00772] The CMA Evolution Strategy: A Tutorial）に従ってPythonでの実装を行います。基本的にどう実装するかの解説がメインの記事ですので、アルゴリズムの理論的詳細についてはチュートリアル論文をご参照ください。

参考文献・実装

[1604.00772] The CMA Evolution Strategy: A Tutorial

http://www2.fiit.stuba.sk/~kvasnicka/Seminar_of_AI/Hansen_tutorial.pdf

The CMA Evolution Strategy

Evolution Strategies による連続最適化

deap/cma.py at master · DEAP/deap · GitHub

Evolution strategies - Scholarpedia

CMA-ES - Wikipedia

アルゴリズム概要

CMA-ESのアルゴリズムをざっくりと示すと下記のようになります。

1. 多変量正規分布 σN(m, C) に従ってλ個体を生成し、各個体の適合度(目的関数の値)を算出する
2. 生成したλ個体のうち目的関数の値が上位μ個体を抽出する
3. μ個体のパラメータと進化パスpσ, pcに基づいて多変量正規分布のパラメータ m、σ、C を更新する
4. 値が収束するまで1-3を繰り返す

最適化の過程を視覚化すると、多変量正規分布（この場合は2次元正規分布）がその形状を伸び縮みさせながら最小値を探索していることが理解できるため直感的にはわかりやすいアルゴリズムです。しかし、いざ実装しようとチュートリアル論文（[1604.00772] The CMA Evolution Strategy: A Tutorial）の疑似コードを見ると登場するパラメータが多すぎて戸惑います。落ち着いて一行ずつ追っていきましょう。

f:id:horomary:20210117230257p:plain:w600 — CMA-ES tutorial, A. Algorithm Summaryより

0. 入力次元数に依存する定数の算出とパラメータ初期化

まずは入力次元数に依存する定数の算出と正規分布および学習パラメータの初期化を行います。

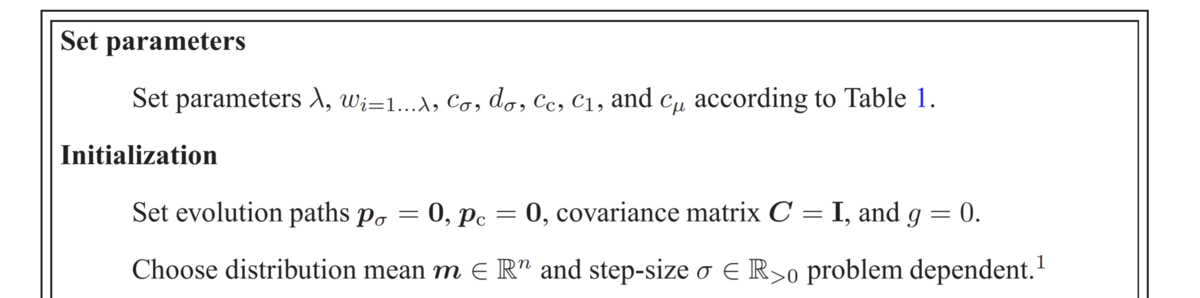
f:id:horomary:20210118232114p:plain:w500

Set parameters で指定されているのは入力次元数に依存する推奨値が設定されている定数パラメータです。これらは調整すべきハイパラというよりはアルゴリズムの一部みたいなものなので強い意図がない限り推奨値を採用するのがよいでしょう。ただし、世代あたり総個体数λだけは大きければ大きいほど良いので許容できる総試行回数と相談して適切な値を設定しましょう。デフォルト値は4 + 3ln入力次元数です。

Initializationで指定されているパラメータのうち、pから始まる $\displaystyle{ p_{\sigma} , p_{c}}$ は入力次元数と同じ長さのベクトルである進化パス(evoluation path)です。進化パスは過去の正規分布中心の遷移情報を蓄積しておくために使用します。

多変量正規分布 $\displaystyle{ \sigma \mathcal{N}(m,C) }$ のパラメータのうち、共分散行列Cは単位行列Iで初期化しますが正規分布中心mおよびステップサイズσは自分で問題に応じて設定する必要があります。最適化したい関数についての事前知識がない場合、中心mは適当でもあまり問題ないですが、σは小さすぎるとすぐに局所収束してしまうので様子を見て調整しましょう。

1. 多変量正規分布に従う個体サンプリング

f:id:horomary:20210118231908p:plain:w500

探索フェーズでは、多変量正規分布 $\displaystyle{ \sigma \mathcal{N}(m, C) }$ に従う個体xをλ個体生成しそれらの適合度（目的関数の値）を評価します。

$\displaystyle{ x \sim \sigma \mathcal{N}(m, C) = m + \sigma \mathcal{N}(0, C) }$ であるので、多変量正規分布 $\displaystyle{ \mathcal{N}(0, C) }$ に従うサンプルを生成することができればxを生成することができます。

$\displaystyle{ \mathcal{N}(0, C) }$ に従うサンプルを生成するもっとも簡単な方法はnumpy.random.multivariate_normalとかを使うことですが、ここでは多次元独立標準正規分布 $\displaystyle{ \mathcal{N}(0, I) }$ の線形変換による多変量正規分布の生成を行います。わざわざ面倒なことをする理由は後述。

具体的には、まず共分散行列Cを $\displaystyle{ C = B D D B^{T} }$ の形に固有値分解します。標準正規分布から生成されたサンプル $\displaystyle{ z = \mathcal{N}(0, I) }$ の線形変換 $\displaystyle{ y=BDz }$ はCを共分散行列とする多変量正規分布に従うため、 $\displaystyle{ y \sim \mathcal{N}(0, C) }$ となります。

なぜこれで多変量正規分布を生成できるかは下記リンクが大変分かりやすく説明してくれていますので参照ください。
多変量正規分布にしたがう乱数の生成 - 捨てられたブログ

いちおうnumpy.randomの多変量正規分布モジュールの結果とだいたい一致することを確認しておきます。

f:id:horomary:20210119003836p:plain:w500

2. 正規分布中心mの更新

まずは正規分布中m心の更新から行います。

f:id:horomary:20210122225141p:plain:w500

$\displaystyle{ x \sim m +\sigma \mathcal{N}(0, C) = m + \sigma y }$ であることから、正規分布中心の学習率 $\displaystyle{ c_m }$ が推奨値の1.0に設定されているとき、現世代の上位μ個体のパラメータの重みづけ平均を次の正規分布中心mとする、という意味になります。

重みづけ平均のための重みwは適合度（目的関数値）の順位が良いほど大きくなるように、かつ重みの総和が1になるように設定します。 この重みwはいくつかの決め方がチュートリアル論文で紹介されていますが、順位iに応じて $\displaystyle{ w_i = \frac{\log{\frac{\lambda}{2}} - \log{i}}{\sum_{i}^{\mu}{w_i}} \ \ ( i = 1 ... \mu ) }$ と設定する方法が無難かつ実装が楽です。

この正規分布中心の更新だけでも進化計算アルゴリズムとして最低限機能します。 しかし、世代ごとの探索範囲が狭すぎるため、大域的な地形を捉えることに失敗し局所地形にトラップされがちであることがわかります。

f:id:horomary:20210119011537g:plain:w500 — 正規分布中心ｍのみ更新

3. ステップサイズσの更新

正規分布中心mの更新だけでは探索範囲が狭すぎて最適化に失敗することがわかりました。そこで、探索範囲に影響するパラメータである正規分布のステップサイズ変数σ を、進化パス $\displaystyle{ p_{\sigma} }$ に応じて更新します。

f:id:horomary:20210120005804p:plain:w500

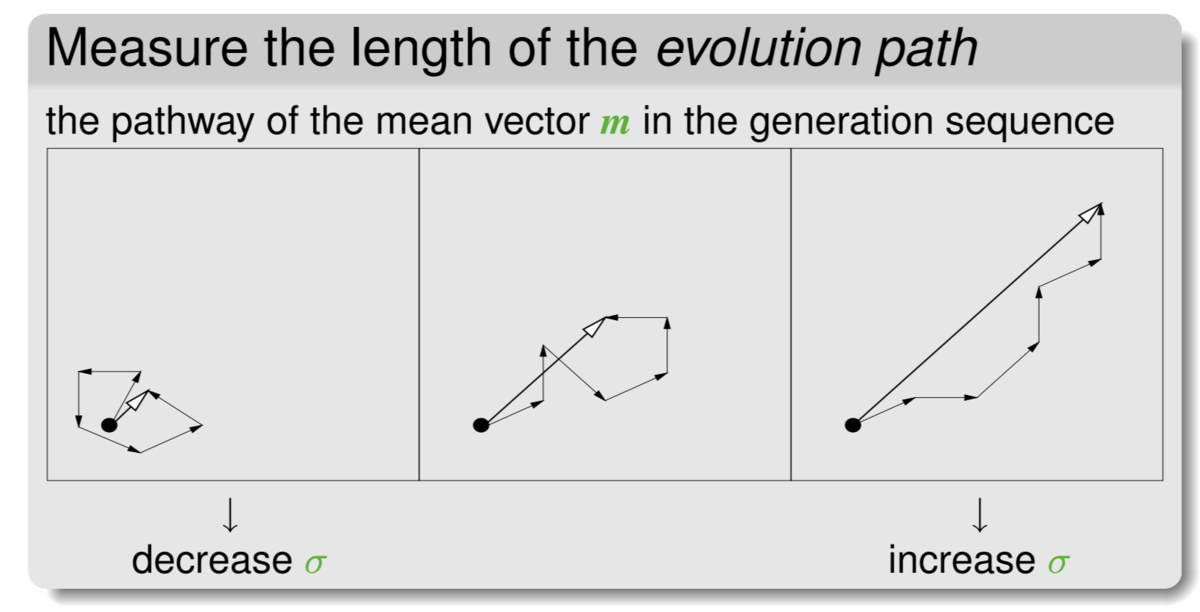
直感的には、進化パス $\displaystyle{ p_{\sigma} }$ とは過去世代での正規分布中心の遷移ベクトルの重みづけ和と理解できます。
指数平滑移動平均の計算と似たような感じで、重みは最近の遷移ほど大きくなります。

もし遷移がランダムウォークしているならば付近の地形がざっくり凸であると判断できるのでσを小さくして探索範囲を絞るべきです。そうではなく遷移に指向性があるならばまだ坂を下っている途中と判断できるのでσを大きく更新する、というのがステップサイズσの更新アルゴリズムの概要です。

f:id:horomary:20210120231904p:plain:w400 — http://www2.fiit.stuba.sk/~kvasnicka/Seminar_of_AI/Hansen_tutorial.pdf, 45p より

実装については、 $\displaystyle{ C^{\frac{1}{2}} y_w= BD^{-1}B^{T} y_w}$ という定義であることに注意しましょう。定義から $\displaystyle{ C^{\frac{1}{2}} y_w = B z_w }$ であり、つまりこれは楕円yを正円Bzに戻す処理なのでノルム計算のための正規化処理と理解できます。※ただし、ここまでの実装だと共分散行列Cは単位行列のまま更新していないのでyもまた正円であることに留意ください。

f:id:horomary:20210121010224p:plain:w500 — チュートリアル論文より

前述した多変量正規分布からの個体発生でnumpy.random.multivariate_normalを使わずわざわざ手動で共分散行列の固有値分解をしたのはこのσの更新ステップで使うからだったのです。

f:id:horomary:20210119011655g:plain:w500 — 正規分布中心mとスケールσを更新

探索範囲を適応的に変更することができるようになったため、なんとか最適解付近にまで到達できています。しかし、このような等方円状探索は入力次元数に指数比例して球体積が増大するので効率が良くありません。とくに目的関数に対する感度が各入力変数で著しく異なるような場合（悪スケール条件）では非常に効率の悪い探索となります。

4. 共分散行列Cの更新

等方円状ではなく、目的関数への感度が高い（変化の大きい）方向について重点的に探索幅が大きくなるように共分散行列Cを更新していくことで悪スケール性の強い目的関数でも効率よく探索することができるようになります。これがCMA-ESがCMA（共分散行列適応）たる所以である共分散行列の適応的更新アルゴリズムです。

f:id:horomary:20210120012713p:plain:w500

まず共分散行列Cの進化パス $p_{c}$ は、ステップサイズσの更新における $p_{\sigma}$ とほぼ同じ形の式であるため過去世代での正規分布中心の遷移ベクトルの重みづけ和と理解できます。唯一異なる $h_{\sigma}$ は、ステップサイズσが大きすぎる時には共分散行列Cの進化パス $p_{\sigma}$ の更新を中止する役割を持ちます。

$\displaystyle{ w_{i}^{o} }$ について、上位個体数μを推奨値通りに決めているならば負の重みは生じず常に $w_{i}^{o} = w_{i}$ なので気にしなくて大丈夫です。

さて重要なのは共分散行列Cの更新式です。第一項は学習率に応じて現在のCを縮小してるだえけの処理なのでとくにコメントはありません。

第二項の $\displaystyle{ c_{1} p_{c} p_{c}^{T} }$ はrank-one updateと呼称される進化パス $p_{c}$ を用いた共分散行列Cの更新処理です。ここで $\displaystyle{ p_{c} p_{c}^{T} }$ は２つのベクトルの直積であることに注意してください。rank-one更新とはこれまでの進化パス（正規分布中心の遷移ベクトルの重みづけ和）の指向性に応じて共分散行列を更新する処理と理解できます。直感的には、（２次元入力なら）正規分布中心の遷移ベクトル方向に沿って楕円（共分散行列）の軸を伸ばしていく処理です。

第三項の $\displaystyle{ c_{\mu} \sum{w_{i} y_{1:\lambda} y_{1:\lambda}^{T}} }$ は、rank-μ updateと呼称される進化パス $p_{c}$ に依存しない共分散行列Cの更新処理です。これは現世代のmを分布中心としたうえでの上位μ個体からの共分散行列の推定であり、有望個体群から推定される共分散行列をCの更新に利用する処理であると理解できます（下図を参照）。rank-μ更新は有望個体群の数μが小さい場合は推定精度が低く効率が悪いことに留意しましょう。