深層分布強化学習 ②QR-DQN
QR-DQNをtensorflow2で実装します。
元論文: [1710.10044] Distributional Reinforcement Learning with Quantile Regression
参考:
https://physai.sciencesconf.org/data/pages/distributional_RL_Remi_Munos.pdf
Going beyond average for reinforcement learning | DeepMind
Quantile regression - Wikipedia
はじめに
DeepMindのDQNに代表される典型的なQ学習においては、状態行動価値Q(s, a)の期待値を関数近似します。
一方、前記事で実装を紹介したCategorical DQN ([1707.06887] A Distributional Perspective on Reinforcement Learning)は、状態行動価値Q(s, a)を明示的に確率分布Z(s, a)としてモデル化することを提案し、これにより大きくパフォーマンスが向上することを当時のatari環境のSotAという結果で示しました。
本記事で紹介するQR-DQNはCategoricalDQNの直接の後継手法*1です。Categorical DQNでは価値分布をそのままカテゴリ分布で近似しようとしたのに対し、QR-DQNは状態行動価値分布Z(s, a)の分位点を近似するというアプローチによりCategorical DQNの残した多くの課題を解決しました。
Categorical DQNの分布モデル
分布強化学習でモデル化したい真の(ground truth?)状態行動価値分布Z(s, a)は連続分布であるはずですが、連続分布は大変扱いづらいのでCategorical DQNではその名の通りZ(s, a)をカテゴリカル分布で近似します。Categorical DQN論文ではカテゴリカル分布のビン数=51の場合がatari環境でもっとも性能が良かったので、この場合をとくにC51と呼称しています。*2
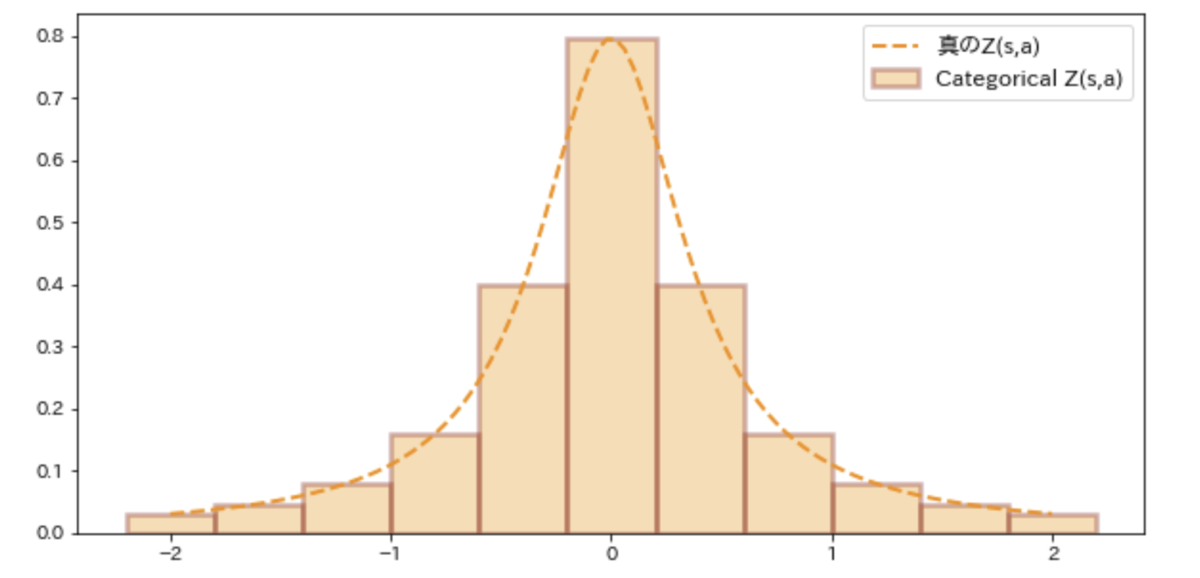
状態行動価値分布Z(s,a)へのベルマンオペレータの適用は下図のように行います。rewardによって分布が水平スライドし、割引率によって分布が縮むようなイメージです。※見た目にわかりやすいようにreward=7, 割引率γ=0.6という極端な値で作図していることに留意ください。
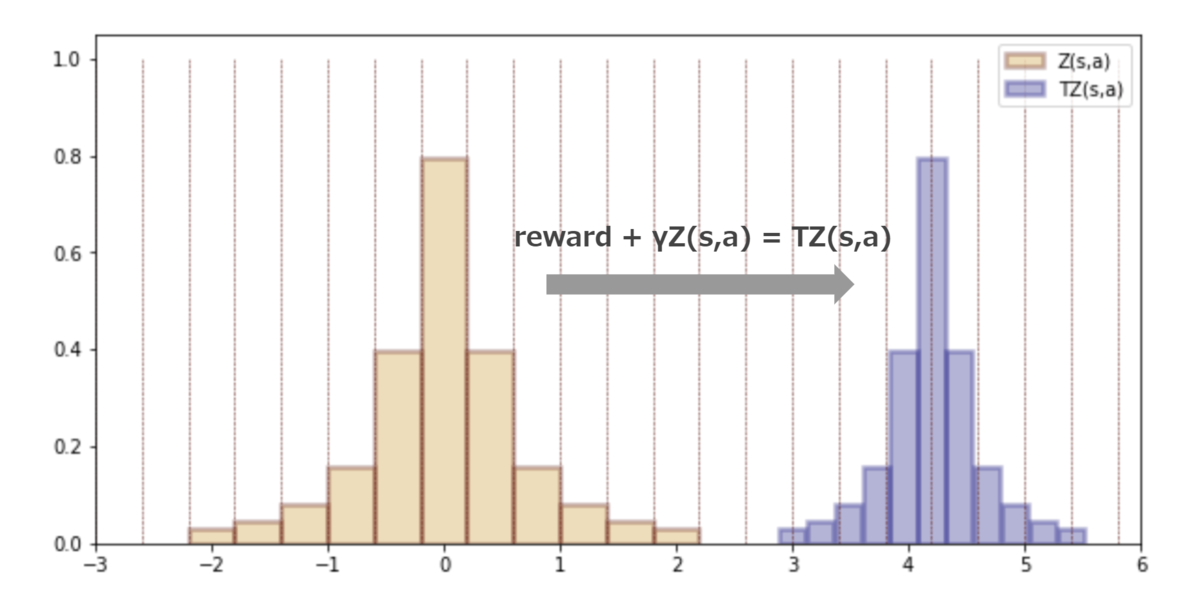
状態行動価値分布をCategorical分布で近似するC51のアプローチはいくつかの大きな問題を抱えています。
1つはベルマンオペレータの適用によって分布のビン幅がずれることです。上図でも元の分布Z(s,a)のビン幅である赤破線からTZ(s, a)のビン幅はずれてしまっていることがわかります。よってCategorical DQNではこのずれたビン幅を無理に再割り当てして修正する処理*3が必要なのですが、この処理の実装がかなり煩雑&やや重い*4です。
別の問題はカテゴリカル分布では有限領域しか扱えないため、分布の最大値/最小値の設定が非常に重要なハイパーパラメータになってしまうことです。 この問題は学習初期と学習終盤で報酬のスケールが大きく変化するような場合には顕著な問題となります *5。また、最大/最小幅を大きくとった場合はカテゴリカル分布の性質上ビンの数を十分に多くしないと細かな分布の形状を捉えにくいという問題も生じます。
さらにCategorical DQNの最大の問題は、Categorical DQN論文で証明された"p-Wasserstein距離を分布間の距離尺度に設定するとベルマンオペレータが縮小写像である"という理論とCategorical分布のKL距離をロス関数とする実装にギャップがあることです。大雑把には、確率的勾配降下法でWasserstein距離をロス関数にすると biased gradient になるので、言っていることとやっていることが違うのだけどKL距離をロスにするヒューリスティックな実装にしたよ、という感じです。( 前記事を参照)
QR-DQNの分布モデル
Categorical DQNではZ(s,a)をそのままカテゴリカル分布で近似しましたが、QR-DQNではZ(s,a)の累積分布関数Fを近似します。※Z(s,a)とその累積分布関数Fは1対1変換であるのでどちらを近似してもよいことに留意。
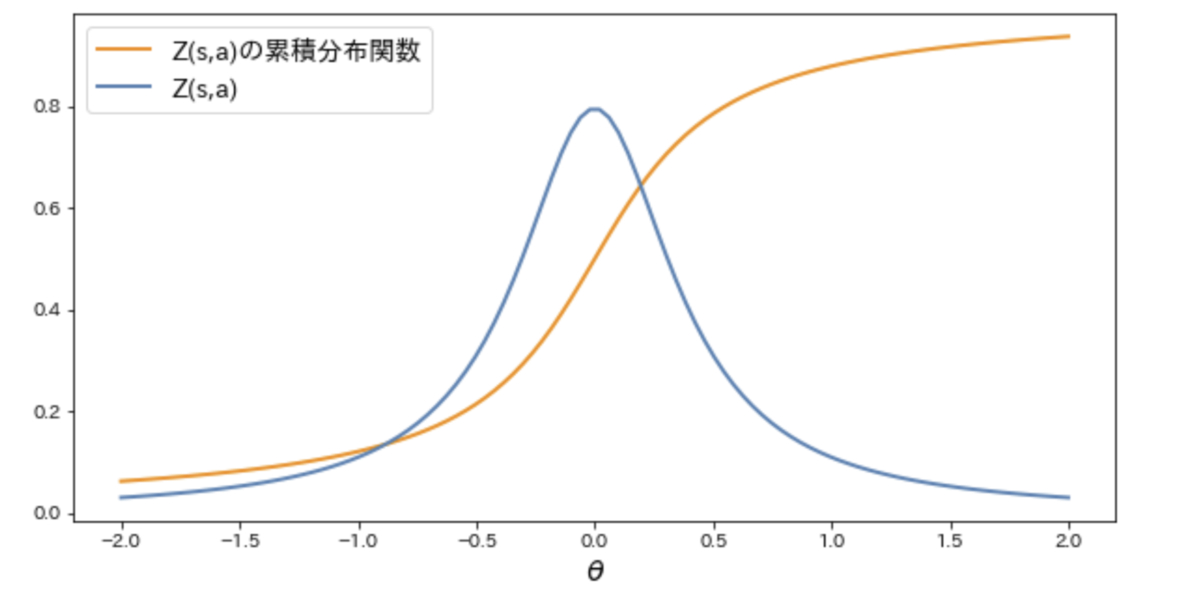
ここで、QR-DQNのポイントは累積分布関数Fそのものではなく、Fの逆関数をカテゴリカル分布で近似することです。
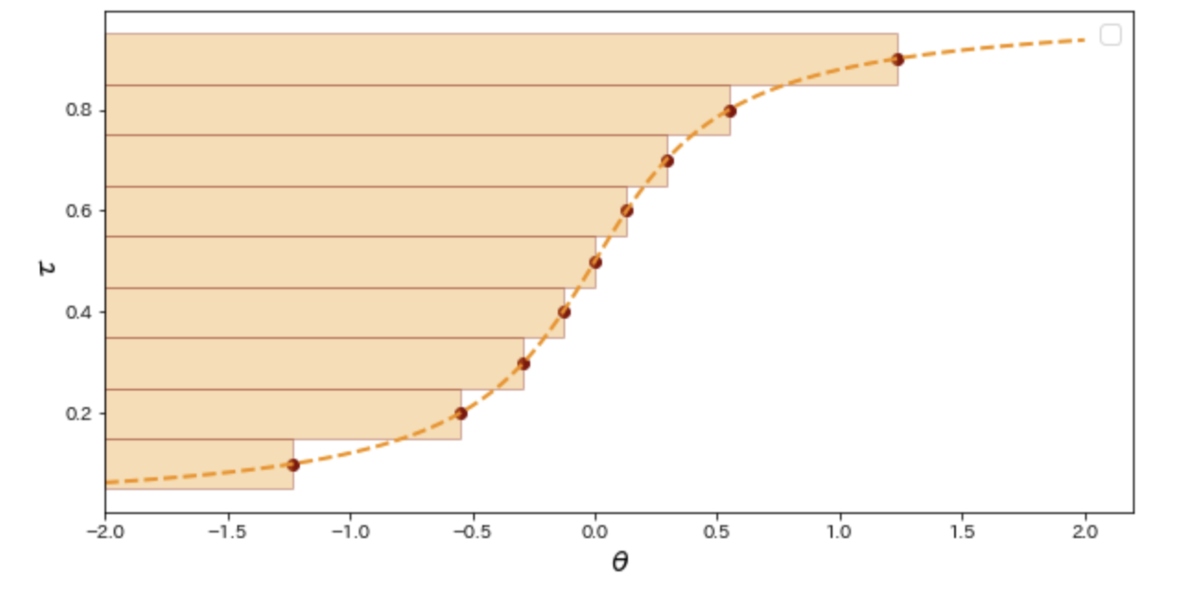
したがって、Categorical DQNでは各ビンの値はZ(s,a)がある状態行動価値θをとる確率でしたが、QR-DQNでは各ビンの値はZ(s,a)の τ%分位点 (Quantile)の値となります。あえてZ(s,a)の累積分布関数の逆関数をカテゴリカル分布で近似することにより、前述したCategorical DQNの問題点を解消することができます。
まず、Categorical-DQNではx軸のカテゴリカル分布でZ(s,a)を近似していましたが、ベルマンオペレータの適用によってビン幅がずれるため煩雑なビンの再割り当て処理(projection)が必要でした。一方、QR-DQNではカテゴリカル分布で価値分布の累積分布関数をy軸にそってモデル化する(つまり累積分布関数の逆関数を近似)ためビン幅ずれ問題に煩わされることは無くなりました(下図)。

また、カテゴリ分布の最大値/最小値の設定に悩まなくてよくなりました。なぜならば累積分布関数の逆関数は0-1の有限区間で定義される関数であるためです。
さらに、Categorical DQN論文の最大の残課題は理論的にはWasserstein距離を最小化したいのだけれども、Wasserstein距離をそのままSGDのロス関数にするとBiased gradientとなってしまうので仕方なく分布間のKL距離を最小していたことです( 前記事を参照)。
そこでQR-DQNではターゲット分布の分位点を予測することが1-Wasserstein距離を最小化することを示し、このためにSGDのロス関数に 分位点回帰を使用することを提案しました。これにより直接Wasserstein距離をロス関数として使用することを回避してWasserstein距離を最小化できます。

分位点回帰
分位点回帰とそのロス関数を簡単に説明します。
分布の70%分位点を予測することを考えます。この分布
の 10%, 30%, 50%, 70%, 90% 分位点を
= [-1.23, -0.29, 0. , 0.29, 1.23]
とします。*6
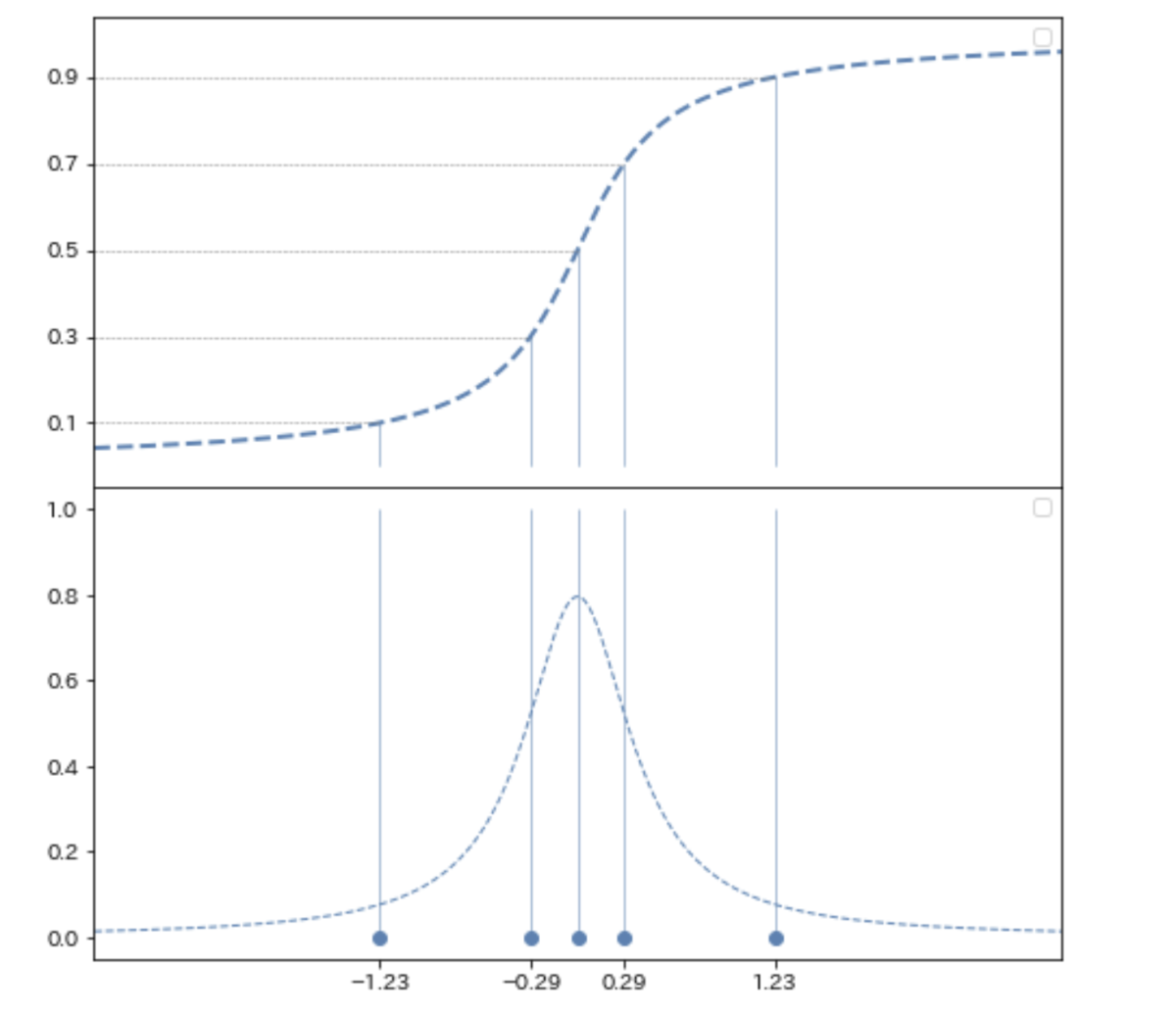
70%分位点の予測値をθと置くと、論文より分位点ロスは下式となります。
※ は
のとき1、そうでなければ0という意味です。
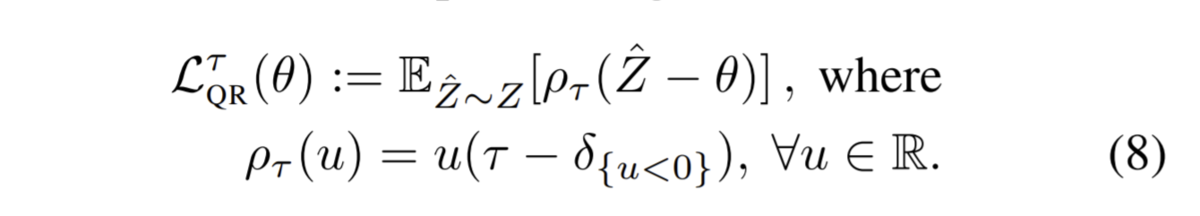
この分位点ロスの視覚的な説明が下図です。ポイントは分布 のすべてのサンプルについて計算した分位点ロス(赤破線で表示)の平均が最終的な分位点ロスであることです。直感的には、予測値θより大きい値との距離総和と予測値θより小さい値との距離総和を予測したい分位点に応じてバランスしているという感じです。
分位点Huberloss
この分位点ロスをニューラルネットのロス関数にそのまま使うとu=0付近で滑らかでないため学習が不安定化するらしく、論文ではQuantile HuberLossを提案しています。と言っても |u|≦1のときは、|u|>1のときは
とただのHuberLossに分位点重みがかかるだけのなので特に難しくはありません。
QR-DQNの実装
Breakout (ブロック崩し)環境向けにQR-DQNを実装します。 ネットワーク構造とネットワーク更新以外はオリジナルのDQNと完全に同じです。
QRネットワークの実装
ネットワーク構造自体はCategorical DQNとまったく同じです。構造は同じですが解釈が違うだけです。
アクション選択もCategorical DQNの場合と同様に価値分布Z(s, a)の平均値が最も大きいactionを選択します。ここで、分位の刻み幅を均等にとっている場合は、E[Z(s,a)]は分位点の単純平均と一致することに留意しましょう。
分位点ロスによるネットワーク更新
やってることは上述の分位点回帰の説明と同じです。しかし、上述の例では70%分位だけを計算していましたがQR-DQNでは設定されたすべての分位についてそれぞれ分位点ロスを計算する必要があるのでけっこう煩雑です。そこで、やってことがわかりやすいようにbatchsize=1の場合を下記に示しておきます。
import numpy as np import tensorflow as tf N = 5 #:分位の分割数 quantiles = np.array([0.1, 0.3, 0.5, 0.7, 0.9], dtype=np.float32) target_quantile_values = np.array([23, 35, 42, 56, 76], dtype=np.float32).reshape(1, -1) quantile_values = np.array([20, 32, 45, 50, 70], dtype=np.float32).reshape(1, -1) target_quantile_values = tf.repeat(target_quantile_values, N, axis=0) quantile_values = tf.repeat(quantile_values.reshape(-1, 1), N, axis=1) td_error = target_quantile_values - quantile_values indicator = tf.where(td_error < 0, 1., 0.) #: k=1.0の場合のhuberloss huberloss = tf.where(tf.abs(td_error) < 1.0, 0.5 * tf.square(td_error), tf.abs(td_error) - 0.5) quantiles = tf.repeat(quantiles.reshape(-1, 1), 5, axis=1) quantile_weights = tf.abs(quantiles - indicator) quantile_huberloss = quantile_weights * huberloss total_quantile_huberloss = tf.reduce_mean(quantile_huberloss, axis=1, keepdims=True) loss = tf.reduce_sum(total_quantile_huberloss, axis=0)
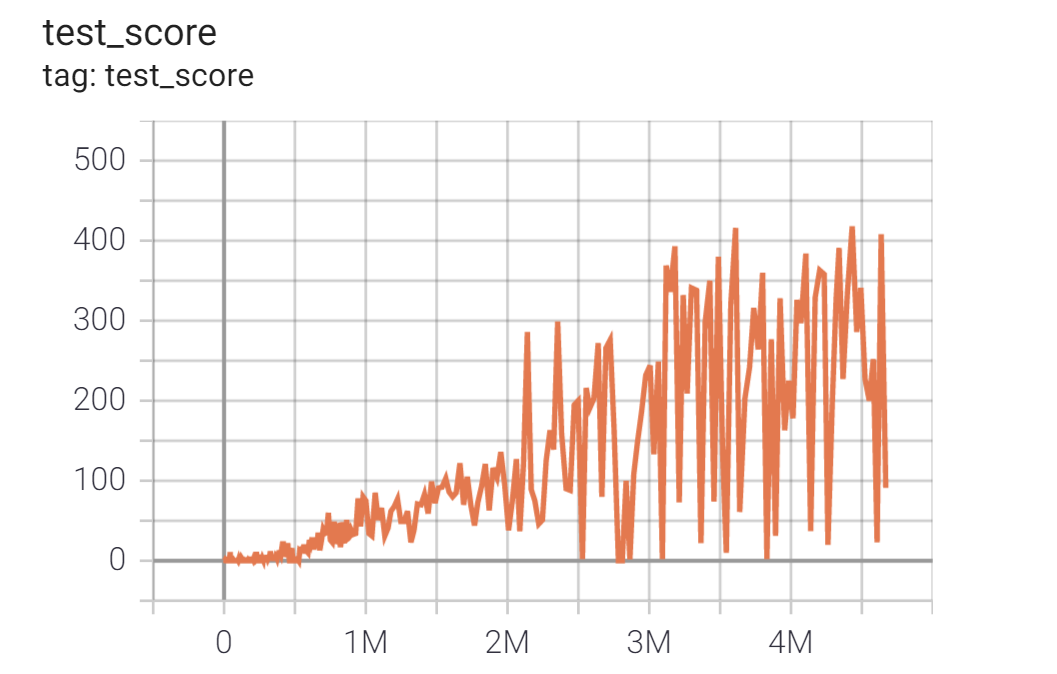
Breakoutでの学習結果
BreakoutDeterministic-v4環境(ブロック崩し)において、GCPのn1-standard-4(4-vCPU, 15GBメモリ) + GPU K80 のプリエンティブルVMインスタンスを使って24時間学習した結果十分なパフォーマンスを確認できました。
Breakoutはatariの中では比較的単純な環境であることを考慮して、Adamの学習率は論文より高め設定のlr=0.00025(論文記載はlr=0.00005) & 分位点の刻み数Nを論文より小さめ設定のN=50(論文記載は分位点の刻み数N=200)にしています。
コード全文: github.com