深層分布強化学習 ① Categorical DQN(C51)
分布強化学習(distributional reinforcement learning)の概念を深層強化学習へ導入したCategorical DQN(C51)をtensorflow2で実装します。
why restrict ourselves to the mean?
― [1707.06887] A Distributional Perspective on Reinforcement Learning

- はじめに
- 分布強化学習 (Distributional Reinforcement Learning)
- Categorical DQN(C51)のtensorflow2実装
- BreakoutDeterminisitc-v4 での結果
- 付録
- 次:② QR-DQN
参考資料
Deep Reinforcement Learning Hands-On | Packt
https://physai.sciencesconf.org/data/pages/distributional_RL_Remi_Munos.pdf
前提手法:Deep-Q-Network (DQN)
horomary.hatenablog.com
はじめに
[1707.06887] A Distributional Perspective on Reinforcement Learning
従来の深層強化学習(Q学習)では期待割引報酬和を最大化するために、状態行動価値Q(s, a)の期待値を関数近似します。Q関数がうまく近似できているならば、Q関数に従って期待値の大きな行動(action)を選択しつづければ報酬和も最大化されます。
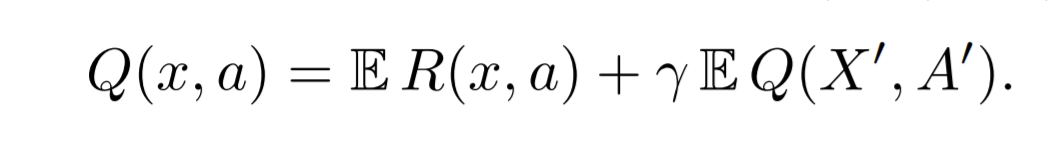
Q関数の期待値が高い行動を選択しつづけること自体は問題ありません。しかし、状態行動価値Q(s, a)の期待値を直接関数近似するのではなく、状態行動価値Q(s, a)の確率分布を関数近似しそこから期待値を算出する方が、Q関数が環境をよく表現できるので学習が安定化するのではないか?というのが論文の要旨です。
この論文ではまずベルマン方程式を分布の概念を導入した分布版ベルマン方程式を提案しました。
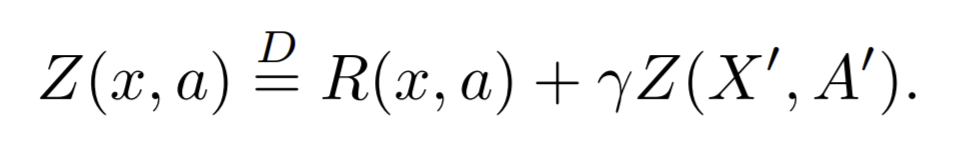
さらに、価値分布をカテゴリ分布で表現したQ学習をatari環境向けに実装し、分布強化学習の有用性を当時のatari環境におけるSOTAという結果で証明しました。atari環境においてはカテゴリ分布のビン数が51に設定されたことから論文内ではこの手法を指してC51と呼称しています。

分布強化学習(distributional reinforcement learning)自体は古くから存在するアイデアだったのですが、 この手法が発表されたことにより深層学習×分布強化学習の研究が活発化し、 QR-DQN, IQN, FQF など多くの後継手法が発表されることとなりました。
※単語が似ていて紛らわしいのですが分布強化学習(distributional reinforcement learning)と分散強化学習(distributed reinforcement learning)は全く異なる概念です。javaとjavascriptくらい違います。
rayで実装する分散強化学習 ①A3C(非同期Advantage Actor-Critic) - どこから見てもメンダコ
分布強化学習 (Distributional Reinforcement Learning)
※論文では状態をxで表記していますがここではsで表記します。また、表記の簡単のために状態遷移は決定論的とします。
通常のベルマン方程式
通常のQ学習では下式のようにベルマンオペレータTを定義し、ベルマンエラー を最小化するようにQ関数を更新していきます。
Q(s, a)はスカラ値なのでベルマンエラー もまたスカラ値であり、この最小化とは一般的な教師あり学習と同様にMSE(平均二乗誤差)*1 なんかを最小化するだけです。
分布版ベルマン方程式
分布版ベルマン方程式では、状態行動価値を期待リターンの確率分布Z(s, a)で表現したベルマンオペレータTを定義します。
遷移先状態s'での行動a'は を最大化する行動を採用します。
であるので、遷移先での行動選択については通常のQ学習と同じです。
通常のベルマン方程式も分布版ベルマン方程式も見た目上はあまり変わりませんが、通常のベルマンオペレータは”スカラ値Q(s', a')に割引率を掛けて即時報酬を足す”、という非常にわかりやすい処理であるのに対して、分布版ベルマンオペレータでは”確率分布Z(s', a')に割引率を掛けて即時報酬を足す”、というやや想像しにくい四則演算を行います。
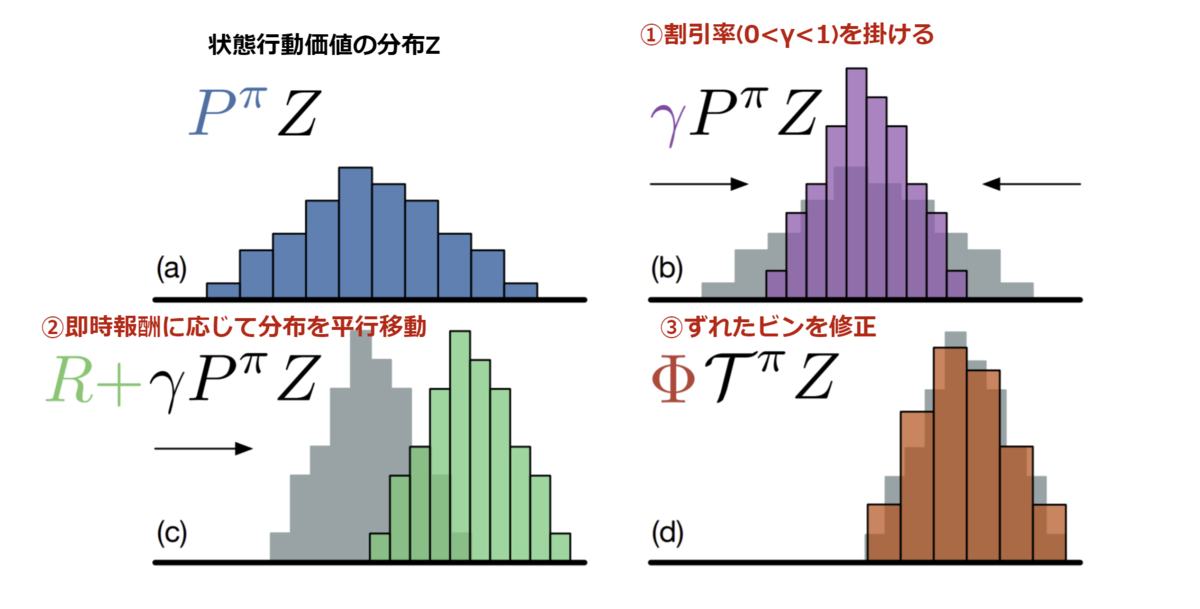
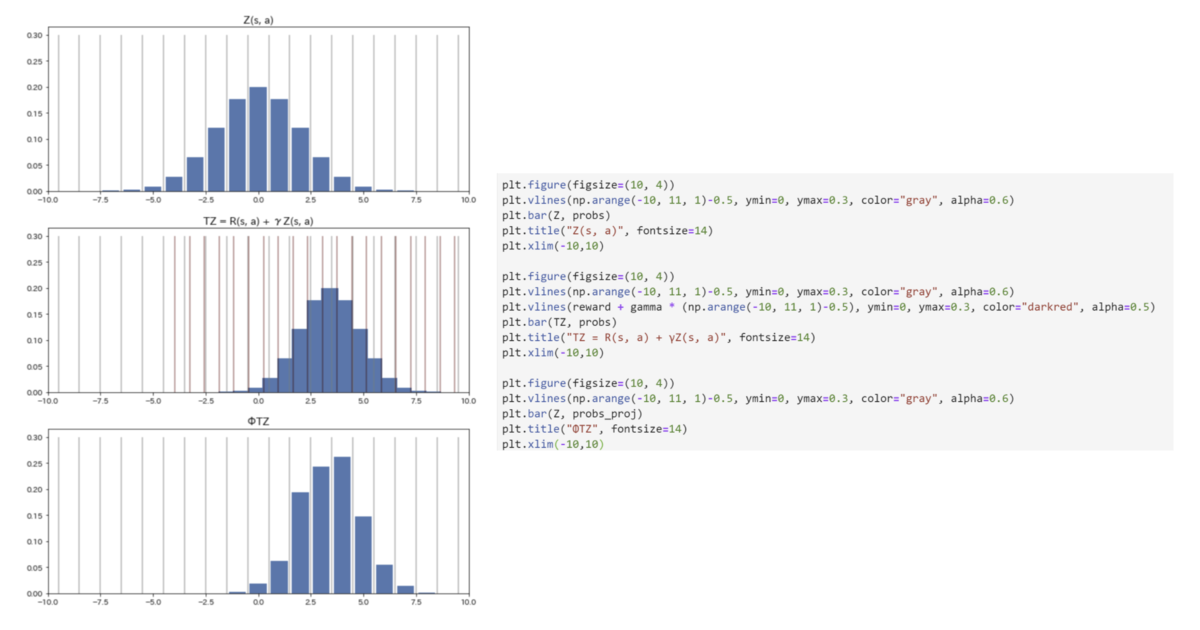
論文内fig.1 はZがカテゴリ分布として表現されている場合での分布版ベルマンオペレータ適用のイメージです。①割引率を掛けることで分布が縮み、②即時報酬が足されることで分布が横に平行移動する、 という処理が可視化されています。(③のずれたビンを直す処理については後述)
同じことをPythonでやってみます。

コードを見ればとくに難しいことはありませんね。
ただし、と
ではカテゴリ分布のビンの幅が変わっていることに注意してください(後述)。
ベルマンエラーの計算(分布版)
ベルマンオペレータ の適用方法がわかったので後はベルマンエラー
を計算するだけです。しかしZは確率分布であるので通常のQ学習のように単純な引き算をすることはできないため、2つの分布間の距離を適切に定義する必要があります。
2つの分布間の距離尺度といえばKL-divergenceやWasserstein-metricなどいろいろありますが、C51ではカテゴリ分布でZを表現しているので深層学習ではお馴染みのcategorical cross entropy を2つの分布間の距離として、これを最小化するようにネットワークを更新していきます。
しかし、上述したようにベルマンオペレータ適用後のはビンの幅が変わってしまっているため、そのままではクロスエントロピーを計算することができません。(灰線がZ(s, a)のビン幅、赤船がTZ(s, a)のビン幅)

そこで、の分布形状を可能な限り保ったまま、
のビン幅に再割り当て(projection)を行う必要があります。この作業を数式にしたのが下式です(論文より)。
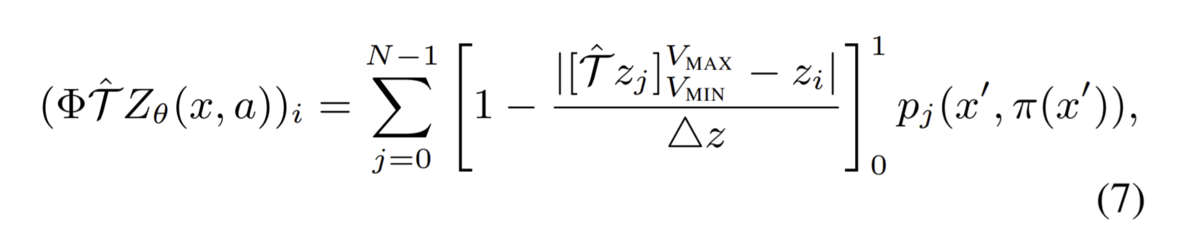
初見では意味不明な数式ですがコードを見るとそれほど難しいことは言っていないことに気が付きます。
ビン幅を再割り当てしたを論文では
と表記しています。ここまで理解できればあとは普通にクロスエントロピーを計算するだけです。
Categorical DQN(C51)のtensorflow2実装
上述した分布版ベルマンオペレータの適用とビンの再割り当て処理(projection)を除くとほぼDQNと同じなので実装の要点だけ掲載。
実装全体はgithubへ:
カテゴリ分布Q関数
ネットワーク構造は基本DQNですが、最終Dense層が"action_space×カテゴリ分布のビン数"のunitsを出力したうえでこれを(バッチサイズ, action_space, n_atoms)にreshapeし、各action軸でsoftmaxをとることで確率分布を表現します。
ちなみに論文ではカテゴリ分布のビンのことをatoms、およびそのビンに割り当てられた確率をsupportと呼称しています。英語だとそういう表現なんですね。
ネットワーク更新
と
のcategorical cross entropyをロスとしてSGDするだけです。
クロスエントロピーの計算はlogをとる前に微小量を加えておかないと打切り誤差でLog(0)を計算してnanを吐くことがあるので注意。(実際2Mstepくらい進んだあたりでnan吐いて学習失敗した)
分布版ベルマンオペレータの適用
上述のコードとやってることは同じですが、ミニバッチ単位での処理のためにややコードの見通しが悪くなっています。
またdoneのときの処理、つまり のときの処理が追加されています。
BreakoutDeterminisitc-v4 での結果
4000エピソードちょいでおよそ400万stepを学習した結果です。
論文の結果(fig.3)を見ると1000万stepくらい学習すればスコアがサチるみたいです。

CategoricalDQN (C51) でbreakoutを攻略。カテゴリ分布版ベルマンオペレータの実装めんどかった。#強化学習 pic.twitter.com/Qux6zQuOCr
— めんだこ (@horromary) 2021年1月6日
マシンはGCPのn1-standard-4(4-vCPU, 15GBメモリ) + GPU K80 のプリエンティブルVMインスタンスを使って24時間学習しました。プリエンティブルVMは激安な代わりに24時間で自動シャットダウンされます。費用はざっくり計400円くらい?
付録
分布ベルマン方程式の理論的保証
本文では価値分布をカテゴリ分布で表現し、categorical cross entropy(※論文ではKL divergenceのクロスエントロピー項と言っている)を分布間の距離尺度とする分布版ベルマンオペレータを天下り的に正しいもののように紹介しましたが、実際はこのような方法の理論的保証はされておらず”APPROXIMATE DISTRIBUTIONAL LEARNING”と明記されています。
[1707.06887] A Distributional Perspective on Reinforcement Learning の前半は分布ベルマン分布の理論的保証に割かれているのですが、ここで保証されているのは固定方策かつZ(s, a)を連続な分布で表現した場合にZ(s, a)とTZ(s, a)の累積分布関数の逆関数のLp-Wasserstein距離を分布間の距離尺度としたときに分布ベルマンオペレータが縮小写像となる(収束する)ということです。
続報でもこのあたりの議論が深められています。
[1902.03149] Distributional reinforcement learning with linear function approximation
しかし、分布版ベルマンオペレータの収束性の話は当然通常のベルマンオペレータの収束性の議論の理解が前提なので、そもそもこのあたりの知識に自信がない人(私です)は、強化学習の青い本(『強化学習』(森村 哲郎)|講談社BOOK倶楽部)2章 プランニング
を読みましょう。
こちらの記事も大変参考になりました。Thank you!
Wasserstein Distance, Contraction Mapping, and Modern RL Theory | by Kowshik chilamkurthy | Medium
経験分布からのWasserstein LossはBiased
上述の通り、論文ではWasserstein距離を分布間距離尺度としたときに分布ベルマン方程式が収束するということを証明したのに、CategoircalDQNの実装ではカテゴリ分布のKL距離を採用しています。これは経験分布のWasserstein距離はBiasedであるためです。
これについてはLemma 7, Proposition 5で説明されていますが、私は理解に時間がかかったので同じような方のために解説しておきます。
具体例として2つの分布PとQの間のwasserstein距離を考えます。分布Pは表(=1)と裏(=0)がどちらも0.5の確率で出るコインの分布(ベルヌーイ分布の確率質量関数)とします。一方、分布Qは表(=1)がpの確率で、裏(=0)が 1-p の確率で出る歪んだコインの分布とします。
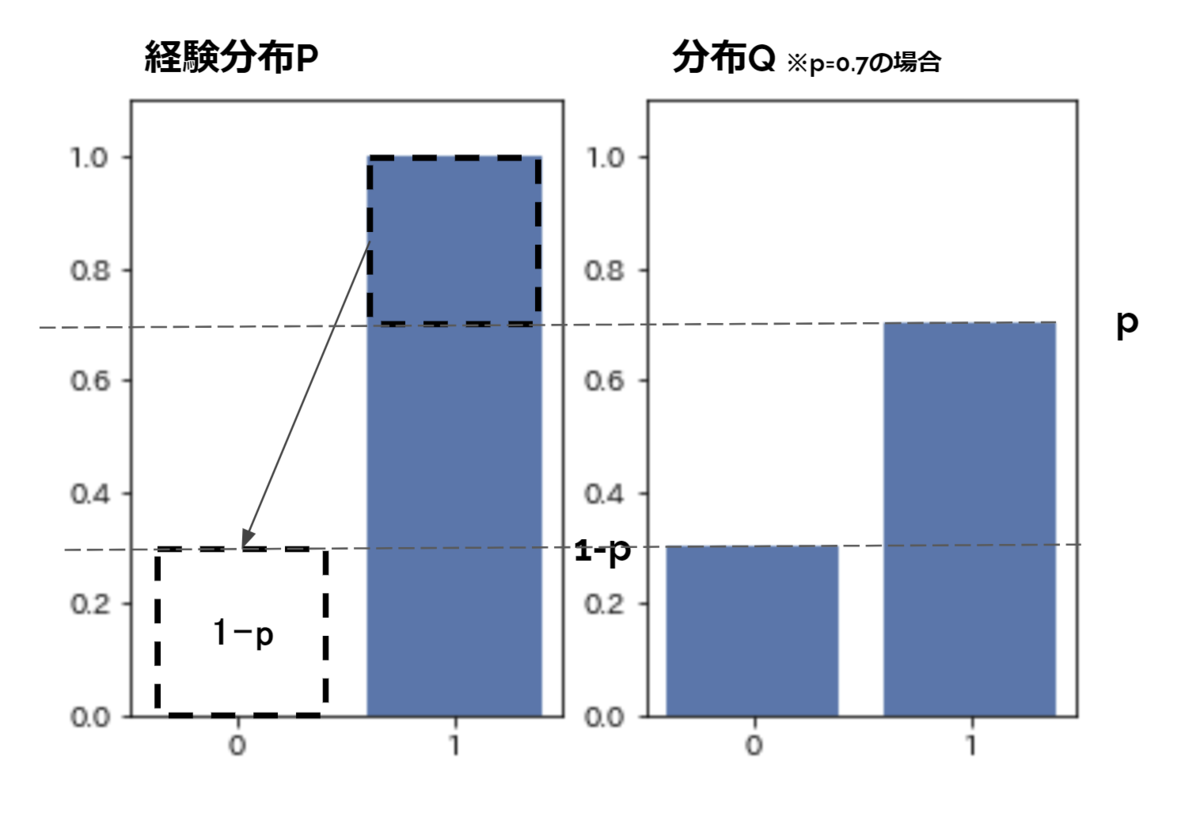
この分布Pと分布Qの1-wasserstein距離 d(P, Q)= |0.5 - p| であることは視覚的にも容易にわかります(下図)。

分布Pは無限のコイントス試行によって得られる真の分布であることに注意してください。もし分布Pが経験分布である場合、極端にはコイントス試行1回行って表が出たという結果からの経験分布の場合、経験分布Pと分布QのWST距離は 1-p となります(下図)。同様に裏が出た場合のWST距離はpとなります。
ここで、PのコインについてN回の試行を行い、各サンプルから得られるPの経験分布と分布QのWST距離のサンプル平均を考えます。表が出る確率は0.5でありこの場合のWST距離は1-p, 裏が出る確率も0.5でありこの場合のWST距離はpであるので、このサンプル平均 E[d(Pi, Q)]は 0.5×p + 0.5×(1-p)= 0.5 となります。上述の通り、分布間の真のWST距離は |0.5 - p| であるので、よってp=0 or 1の場合を除いて経験分布からのWasserstein距離にバイアスがかかることが理解できます。
SGDにおいてミニバッチを構成する各サンプルはまさに報酬分布R(s)および遷移分布P(s' | s, a)からの1回のサンプリングから得られた経験分布であるため、各サンプルのWST距離のミニバッチ平均もまた同様にBiasedとなります。
なぜ分布の推定が学習を安定化させるか?
atari2600環境で当時のSOTAを達成し単体のDQN拡張手法としては最良の結果を示したCategorical DQNですが、状態行動価値分布を推定することでなぜ学習が安定するのかについてはdiscussion項で考察されているものの明確な結論は示されていません。
強化学習の青い本(『強化学習』(森村 哲郎)|講談社BOOK倶楽部)8.2.1.4 カテゴリDQN法 でも、
性能改善の要因として、マルチタスク学習のように目的タスク(期待リターン推定)の学習と並行して関連する多数のタスク(リターン分布推定)を学習することによる効果などが考察されていますが、いまだ議論の段階で、今後さらなる解析が期待されます。
と、述べられています。
他にはこちらの記事も参考になりました。
https://clarelyle.com/posts/2019-02-08-aaai.html
マウスの脳は分布強化学習を行うか?
最近出たDeepmindとハーバード大のNature論文。マウスのドーパミン細胞における神経活動の測定から分布強化学習っぽさを示す結果が得られたらしい。興味ある方はどうぞ。