どこから見てもメンダコ

軟体動物門頭足綱八腕類メンダコ科

スッキリわかるAlphaZero

The game of Go has long been viewed as the most challenging of classic games for artificial intelligence
囲碁はAIにとってもっとも困難なボードゲームの一つと考えられてきました
(Mastering the game of Go with deep neural networks and tree search | Nature より)

Alpha Zero： https://science.sciencemag.org/content/362/6419/1140.full?ijkey=XGd77kI6W4rSc&keytype=ref&siteid=sci (オープンアクセス版)

Alpha Go Zero： Mastering the game of Go without human knowledge | Nature (オープンアクセス版)

DeepMindブログ： AlphaZero: Shedding new light on chess, shogi, and Go | DeepMind



AlphaZeroとは

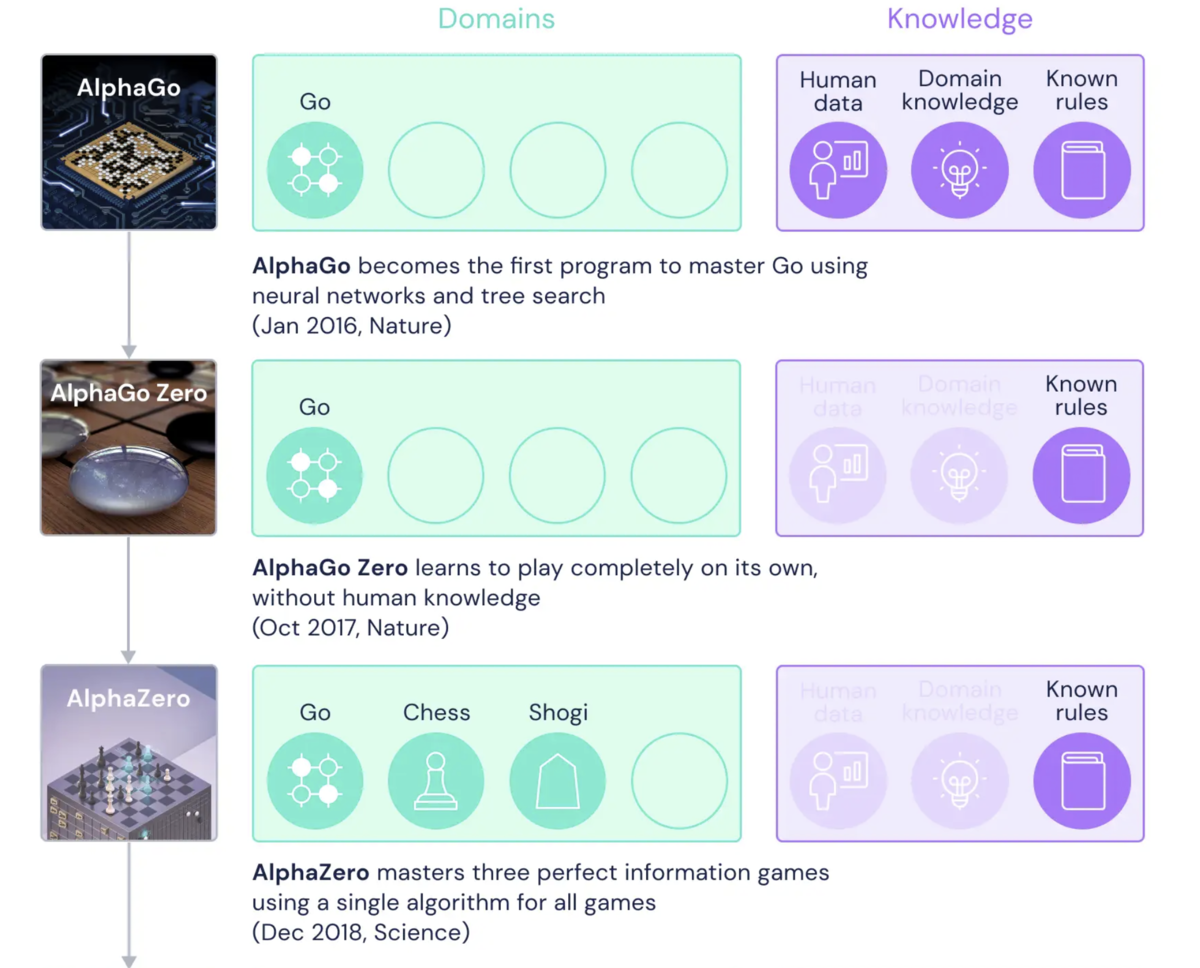
AlphaZero（2018）とは人間の対局データや定石の知識（human knowledge）を使わずに学習を行うボードゲームAIであり、2015年に世界で初めてプロ囲碁棋士に勝利した囲碁アルゴリズムAlpha Goの後継手法です。Alpha Goの”プロ棋士に勝利”という実績はAIの時代を感じさせるわかりやすいインパクトがありましたが、AlphaGoのパフォーマンスは大量の棋譜およびドメイン知識に基づくヒューリスティクス*1に強烈に依存しており、いわゆる"強いAI"からははるか遠いものでした。

このAlpha Goの後継手法であるAlpha Go Zeroでは棋譜すなわち人間の対局データを使わずに、自己対局（selfplay）のみでAlpha Goを超える性能を実現することに成功しました。また、Alpha Goで採用されていた囲碁のドメイン知識に基づくヒューリスティクスも除外されました。

さらにAlpha Go Zeroは微調整され、 AlphaZero として再発表されました。AlphaZeroは Alpha Go Zeroとほぼ同じアルゴリズムをチェス、将棋向けに汎用化したよ、という内容ですので、アルゴリズム的には Alpha Go Zero ＝ AlphaZero という理解で問題ありません。

ただし、事前知識ゼロとは言ってもAlphaZeroにはゲームのルールブックが与えられている、すなわち

  1. ある局面における可能な手（合法手）を問い合わせることができる
  2. ある盤面である手を選択したときの次盤面（盤面の遷移）を問い合わせることができる

ということには留意ください。

f:id:horomary:20210613232914p:plain:w500
MuZero: Mastering Go, chess, shogi and Atari without rules | DeepMind より切り抜き

AlphaZeroは事前データおよびドメイン知識なしで囲碁/チェス/将棋において超人的パフォーマンスを達成したことにより世界に大きなインパクトを与えましたが、真に驚くべきはそのアルゴリズムのシンプルさです。本記事ではこのAlphaZeroアルゴリズムを簡単に解説しつつオセロ向けの実装を紹介します。


アルゴリズム概要

囲碁のような完全情報ゲームにおける理論上最強のアルゴリズムはゲーム木の全探索です。完全探索されたゲーム木を用意できればそこからの検索によって常に最善手をとりつづけることができるためです。

f:id:horomary:20210619193144p:plain:w400
wikipedia: ゲーム木 より

しかし、囲碁や将棋ではゲーム木サイズが巨大であるため*2、全探索は実質的に不可能です。

そこで、AlphaZeroの登場以前から囲碁AIではモンテカルロ木探索（MCTS: Monte-Carlo Tree Search）というゲーム木探索アルゴリズムが中心的に使用されてきました。モンテカルロ木探索とは、"ある盤面がどれだけ良いか"をその盤面から始まる無数のランダムプレイの結果から評価することによって行動決定を行うアルゴリズムです。盤面評価がランダムプレイのみに依存するために盤面評価関数の設計不要であることが特徴です。

モンテカルロ木探索を利用したゲームプレイの流れは下図のようになります。すなわち、その盤面におけるすべての可能な行動（合法手）について遷移先の盤面をモンテカルロ木探索によって評価することによって行動を決定するというものです。ゆえにモンテカルロ木探索は人間が思考内で行う先読みのようなことを行っています。

f:id:horomary:20210619180806p:plain:w600
MuZero: Mastering Go, chess, shogi and Atari without rules | DeepMind の図を改変して掲載

AlphaZeroもまたモンテカルロ木探索を中心としたアルゴリズムであり、その貢献はモンテカルロ木探索に深層学習を導入することによって探索パフォーマンスの大幅な向上に成功したことです。より具体的にはAlphaZeroではselfplay（自己対戦）によって生成された対局データからの教師あり学習によって明らかに筋の悪い手を足切りすることでモンテカルロ木探索を効率化・高精度化します。


Step by stepで理解するAlphaZero版モンテカルロ木探索

参考資料：
モンテカルロ⽊探索の理論と実践
コンピュータ囲碁研究の歩み
モンテカルロ木探索 - Wikipedia

AlphaZeroの中心にあるのはモンテカルロ木探索（MCTS）であり、MCTSを理解することがそのままAlpha Zeroを理解することです。ここではもっとも単純なモンテカルロ木探索のアルゴリズムから始めて、AlphaZero版MCTSに至る過程を３目並べを題材にステップ by ステップで解説します。

※各手法名は必ずしも正式なものではなく、説明の便宜上てきとうに命名したものが含まれていることに留意ください

1. 原始モンテカルロ木探索

まずはもっとも単純な原始モンテカルロ木探索（pure Monte-Carlo Tree Search）を理解しましょう。

f:id:horomary:20210619221037p:plain:w400

３目並べにおいてあなたが先手（黒）だとします。現在の盤面には何も置かれていないので有効なアクションは(左上, 上, 左上, 左, 中央, 右, 左下, 下, 右下)の計９つです。さて、このうちどのアクションを選択するのがよいでしょうか？

単純モンテカルロ木探索では、この９つのアクションそれぞれの次盤面から始まるランダム対局を無数に行います。ここでは、たとえば各アクションについて100回ずつランダム対局を行ったとします。

※ランダム対局ではゲームが終了するまで相手も自分もランダムに行動選択を行います。

f:id:horomary:20210619223159p:plain:w400

９つの合法手のそれぞれについてランダム対局を100回行ったところ、初手は中心に石を置くのが勝率60%でもっともよい結果となりましたので*3、現状の盤面では中心に石を置くのが最善手と判断するというのが単純モンテカルロ木探索のアルゴリズムの全てです、本当に単純ですね。あまりにも単純なアルゴリズムですが、"盤面の良さ"の評価がランダム対局のみに依存しゲームに関する一切の事前知識や評価関数設計が必要ないので、評価関数を設計しにくいゲームでは非常に有効に機能します。


2. UCT-原始モンテカルロ木探索

原始モンテカルロ木探索の大きな欠点はすべての合法手について均等な回数のランダム対局（以下ではプレイアウトとも呼称）を行わなければならないことです。

ランダムプレイである以上、盤面評価の信頼性を確保するためにはある程度の試行回数が必要です。しかし、それでは３目並べのような合法手が少ないゲームならともかく囲碁のような合法手が多い（たとえば囲碁の初手は361通り）ゲームでは膨大な回数のプレイアウトが必要になってしまいます。

そこで導入するのが多腕バンディット問題の考え方です。多腕バンディット問題とは多数のスロットマシーン（バンディットマシン）から有限の試行回数で高設定の台を見つけ出すための理論です。これをモンテカルロ木探索に適用すると、有限のプレイアウト回数でできるだけ良い評価値が得られる行動を見つけ出したい、という問題設定になります。

Vol.31.No.5(2016/9)多腕バンディット問題 – 人工知能学会 (The Japanese Society for Artificial Intelligence)
バンディット問題の理論とアルゴリズム (機械学習プロフェッショナルシリーズ)


ゲーム木探索においてはバンディット問題の有名手法であるUCBアルゴリズムのゲーム木への応用であるUCT（Upper Confidence bound applied to Trees）アルゴリズムがしばしば使用されます。UCTアルゴリズムではすべての合法手についてまずは最低一回評価した後は、次式で定義されるUCTスコアが最大のアクションを選択することでモンテカルロ木探索の効率を向上させます。

f:id:horomary:20210620012618p:plain:w800
Monte Carlo tree search - Wikipedia

\displaystyle{ \text{アクションa'の選択確率} = \frac{\text{アクションa'のプレイアウト累計勝利数}}{\text{アクションa'の累計試行回数}} + c \sqrt{ \frac{ \ln{\text{累計試行回数}} }{ \text{アクションa'の累計プレイアウト回数} } } }

右辺第一項は勝率であり、第二項は全体の試行回数に占めるそのアクションの試行回数割合が小さいほど大きくなるので、プレイアウトの勝率実績が高い（活用）が、あまりプレイアウトされていないアクション（探索）を優先的に選択するアルゴリズムとなります。なお、cは探索と活用をバランスするパラメータです。

では具体例を見てみましょう。下図はさきほどの三目並べの例においてUCTアルゴリズムに従い10回のプレイアウトが終わった状態です。

f:id:horomary:20210620015940p:plain:w600

計算されたUCTスコアが最も高い行動は中央配置の1.47なので次の試行、すなわち11回目の試行ではこの盤面からのプレイアウトを行います。

このようにUCTスコアに従い十分な数のプレイアウトを行うと最終的にはプレイアウト勝率のもっとも高い盤面をもっとも多く試行することになります*4。よって、UCT-原始MCTSの最終的な結論としては試行回数（プレイアウト回数）のもっとも多いアクションを最善手とします。


3. PUCT-モンテカルロ木探索

上述したUCT-原始モンテカルロ探索にさらにN手先読みの要素が追加されることでPUCT-MCTSとなります。ちなみに、一般に”モンテカルロ木探索”と言ったらこのPUCT-MCTSを指すことが多いかと思います。

原始モンテカルロ木探索では”一手読み”しか行いませんが、より深く先読みすることでよりゲーム終端に近づくのでプレイアウト（ランダム対局）の信頼性も高まっていきます。 とはいえ先読みはすればするほど評価しなければいけない盤面が増えるので、先読みを行うのはある程度有望な行動に限定したいところです。

そこでPUCT-モンテカルロ木探索では試行回数が一定回数に到達した盤面のみ、さらに次の盤面を展開します。下図ではたとえば子盤面を展開する閾値を10回の試行としています。

f:id:horomary:20210620111651p:plain:w500

UCT方策によって子盤面が展開済みの盤面が選択された場合は、子盤面のUCTスコアを算出しUCTスコアのもっとも大きい子盤面からプレイアウトを行います。もしその子盤面がさらに子盤面を展開済みであれば、展開されていない盤面を見つけるまで同じことを繰り返します（下図）。

f:id:horomary:20210620113929p:plain:w500

ここで注意すべきは、子盤面からのプレイアウトの結果はその親盤面にも逆伝播すること、さらに囲碁のような２人ゲームでは（当然ではありますが）勝ち/負けのカウントはその盤面が先手番か後手番かで逆になることです。

ここまでで、有望な行動に多くの試行回数を割りあてつつ、十分に有望な手に限ってはさらに深い先読みを行うことで効率的にゲーム木を探索するPUCT-モンテカルロ木探索を説明しました。ここまで理解できればAlphaZero-モンテカルロ木探索の理解までもう少しです。


4. PUCTモンテカルロ木探索＋エピソード記憶

UCTアルゴリズムは効率のよい探索手法ですが、毎回知識ゼロからのMCTS開始を強いられる、というつらみがあります。とくに囲碁や将棋のような合法手の多いゲームでは致命的につらいので、過去のモンテカルロ木探索の履歴をうまく利用して筋の悪い手を足切りできないかということを考えます。

たとえば、100回ゲームをプレイすれば少なくとも初期盤面から始まるMCTSについては100回行っているので筋の良い/悪い初手のあたりはつくはずです。このような過去のMCTSの履歴から考えて明らかに有望でない手は試さなくてもいいよね、というようにepisode contextを活用したくなります。

Multi-armed bandits with episode context | SpringerLink

このコンセプトを実現するためにはどうすればよいでしょうか？

たとえば、ごく単純なやり方としてエピソード（ゲーム）をまたいで盤面ごとのMCTS試行回数を記録しておく方法が考えられますが、この方法は可能な盤面の多いゲームではつらいですし、ほんの少し盤面が異なるだけで使えなくなってしまいます。

そこで、AlphaZeroでは過去のモンテカルロ木探索の結果を近似（再現）するようなニューラルネットワークを構築します。 つまり、ある盤面を入力として、過去のMCTSの結果を出力するように教師あり学習で訓練します。

f:id:horomary:20210620162645p:plain:w500
Alpha Go Zero論文 Fig.1を改変して掲載

このように、過去のモンテカルロ木探索の結果を近似するネットワークを訓練することで、有望な手とそうでない手のあたりをつけることができるようになりました。このニューラルネット方策 P(s, a)をUCTスコアに組み込みます。（C_puctはハイパラ）

f:id:horomary:20210620163100p:plain:w400

U(s, a)ではUCTスコアの第二項にP(s, a)を掛けており、過去のMCTS試行の記憶であるP(s, a)がMCTSの事前信念のような役割を担っていると解釈できます。

なお、行動選択ではUCTと同様に、活用 Q(s, a) と 探索 U(s, a) の和が最大の行動を選択します。

f:id:horomary:20210620163223p:plain:w300

このようにAlphaZeroではPUCT-MCTSに過去のMCTS試行情報（episode context)を反映することで、さらに効率よくゲーム木を探索できるようになります。

ところで、ここまでの手法では Q(s, a) とはプレイアウト（＝ランダム対局）の勝率でした。しかし、AlphaZeroではこの項もまたニューラルネットワークで置き換えます。


5. PV-モンテカルロ木探索（AlphaZero）

エピソード記憶に基づく事前信念付きPUCTアルゴリズムの導入によって探索効率は劇的に改善されますが、盤面の良さの評価はいまだにランダム対局（プレイアウト）に完全に依存しています。プレイアウトでは盤面評価関数の設計をせずに盤面を評価できる良さはありますが、人間はランダムプレイするわけではないのでやはり評価精度に限界があります。よい盤面評価関数が利用可能なら本当はそっちを使いたいのです*5。

そこで、Alpha Zeroではある盤面Sを入力としその盤面Sが最終的に勝利したか敗北したかをラベルとする教師あり学習によってニューラルネットワークを訓練し、盤面の評価関数V(s) とします。すなわち、V(s)が1.0に近いほど勝ちそうな盤面ということです。

これによりプレイアウト（ランダム対局）をニューラル盤面評価関数Vで置き換える*6ことで、盤面の良さの評価精度もまた大きく改善することとなりました。


AlphaZeroのMCTSまとめ

・過去のモンテカルロ木探索の履歴をニューラルネットで近似し、方策の事前分布としてPUCT-MCTSへ導入
→ 筋の悪い行動の足切りを行いMCTSの効率化を実現

・過去のある盤面の最終的な勝敗結果をニューラルネットで学習し、盤面評価関数Vとする
→ MCTSによる行動評価の高精度化を実現

この２つのネットワークを備えたMCTSがAlpha Zeroのモンテカルロ木探索であり、論文ではPV-MCTS (Policy Value - MCTS)と呼称されています。そして２つのネットワークを訓練するためのデータはすべて Selfplay (自己対局) によって生成されるため人間のナレッジを一切必要としません。これがAlphaZeroのすべてです、なんとシンプルなアルゴリズムでしょうか。


Policy-Value ネットワークについて

上述のMCTS説明では、過去のMCTS履歴を近似するニューラル方策関数(Policyネットワーク)と盤面評価関数(Valueネットワーク)は別のもののように書きましたが、実際はパラメータを部分共有する双出力ネットワーク（下図）になっています。

f:id:horomary:20210620182615p:plain:w200
パラメータを部分共有するネットワーク構造

このようなネットワーク構造はモデルフリー強化学習手法のA3Cでもお馴染みであり、視覚情報をそのまま入力するようなネットワークでは入力画像の表現抽出を担う部分をマルチタスク学習することでロバストな特徴表現が得られる（だろう）ために、強化学習エージェントのパフォーマンスが向上することが経験的に知られています。

rayで実装する分散強化学習 ①A3C（非同期Advantage Actor-Critic） - どこから見てもメンダコ


盤面状態の入力形式

盤面状態をどのような形式でニューラルネットに入力するかについて、alphazero論文の記載がややわかりづらいので補足説明します。囲碁も将棋もチェスもちゃんとルールわかってないので間違ってる場所あるかも。

f:id:horomary:20210620183524p:plain:w500
Alpha Zero論文より

囲碁：
囲碁では19×19の平面（碁盤に対応）を17枚重ねることで盤面状態を表現しニューラルネットへの入力とします。17枚の平面の内訳は（自分の石配置を1としそれ以外を0とした平面, 相手の石配置を1それ以外を0とした平面）× 直近8step分 ＋ (自分の色が黒ならすべて1で白ならすべて0の平面) となっています。

直近8step分を入力するのは同じ手の反復を検出するため、自分の色情報を含めるのは”コミ”への対応のため記述があります。

チェス・将棋：
チェスでは8×8の平面（チェス盤に対応）を119枚重ねることで盤面状態を表現しニューラルネットへの入力とします。119枚の平面の内訳は（[自分のポーンの配置を1としそれ以外を0とした平面,、同様にルーク、同様にナイト、同様にビショップ、同様にクイーン、同様にキング]、[同様に相手の各駒の配置] + その盤面をすでに1回見たかどうかを示す平面 + その盤面をすでに2回見たかどうかを示す平面）× 直近8step分 ＋ (自分の色が黒ならすべて1で白ならすべて0の平面) + チェスの特殊ルールを表現した平面×６ となっています。

チェスと将棋は単純な反復手の禁止に加えて、ゲーム中に同じ盤面が３回出たら流局のルールがあるためその盤面の出現回数を表現する平面があることに留意してください。

将棋も基本はチェスと同様ですが、持ち駒(prisoner)や成り駒によって表現が煩雑になっています。たとえばP1 piece（自分の駒）の14平面というのは、（記事を修正）自分の歩、香、桂、銀、金、飛車、角、王の配置を示す平面７枚に加えて、各駒を持ち駒として保持しているかを示す平面７枚。これに加えてP1 prisoner countの７平面で各駒を何枚持っているかreal valueで示しているのだと思います（ちがうかも）。 自分の駒の8種類[歩,香車,桂馬,銀,金,角,飛車,王]に成駒[成歩,成香,成桂,成銀,馬,竜]の6種類を加えたものとなります。

とくに将棋についてはこんな無理やりな盤面表現でも学習するんだから深層学習大したものだなと思います。


ニューラル方策関数の出力形式

同様にニューラル方策ネットワークの出力形についても解説します。

f:id:horomary:20210620183633p:plain:w500
alphazero論文より

囲碁：
囲碁は19×19×1の平面で行動を表現します。平面の各要素は碁盤の対応する場所に石を置く確率を示します。

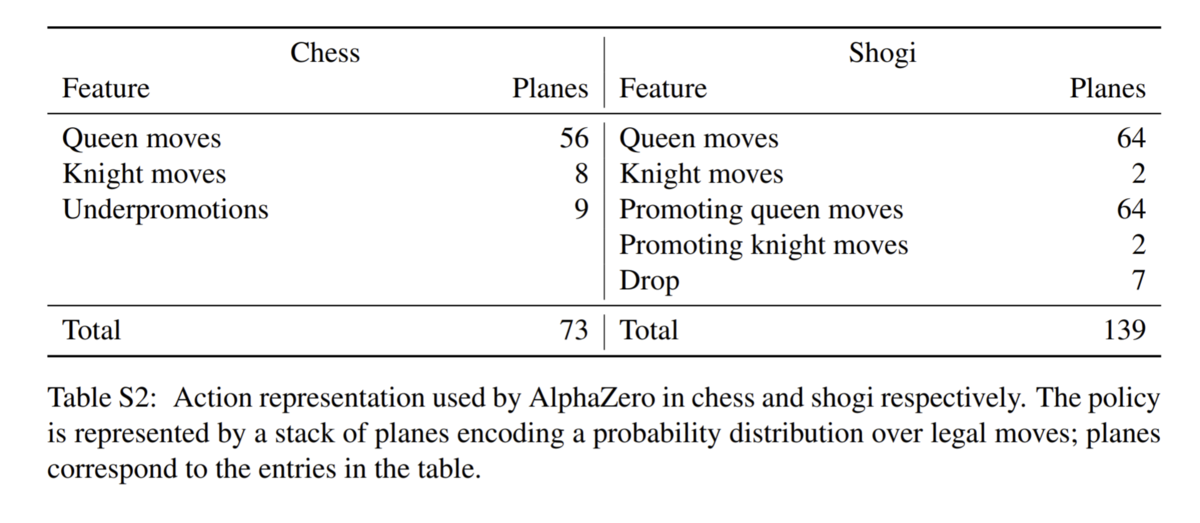
チェス・将棋：

チェスでは８×８の平面を73枚重ねることで行動を表現します。８×８で盤上のどの位置に置いてある駒を動かすかを表現し、73次元でどのように動かすかを表現します。たとえば下の盤面における方策出力をPとします（P.shape == (8, 8, 73) ）。

f:id:horomary:20210620214213p:plain:w300
P[7, 2, 9]の行動

ここで、P[7, 2, 9] == 1.0 のとき、(7, 2)に対応する(1, c)に存在する駒（ビショップ）が73種類の動きのうち9番目の動きを行うことを意味します。12番目の動きは56種類（8方向×7マス）で表現されるQueen move、すなわち上下左右斜めの8方向に1-7マスのいずれかです。素直に上から{0, 1, 2, 3, 4, 5, 6}, 次に右斜めを {7, 8, 9, 10, 11, 12, 13} としていた場合は、P[7, 2, 9] == 1.0は(1, c)に置いてある駒を右斜め上に3つ移動させるという行動となります。


AlphaZeroの実装

ここからはオセロを題材としたAlphaZero実装の解説を行います。オセロはゲームの進行につれて行動の自由度が減っていくためMCTSと相性が良く、それほど苦労せずにsuperhumanな性能に到達することができます。

コード全文：
github.com


トレーニングループ

AlphaZeroのトレーニングの流れはごく単純で、

  1. N回のselfplayによりデータ収集
  2. 収集したデータでネットワークを更新

のループを繰り返すだけです。

※自己対局（selfplay）の繰り返しはPythonの並列処理ライブラリrayで並列実行しています。

Pythonの分散並列処理ライブラリRayの使い方 - どこから見てもメンダコ



Selfplay（自己対局）

Selfplayもそれ自体は特筆することはありません。モンテカルロ木探索での試行回数に応じて行動決定することをゲーム終了まで繰り返します。


PV-MCTSの実装

Alpha Zeroの中心であるPV-MCTSの実装です。PV-MCTSそのものを理解していればプログラミング的には特段難しいところはありません。

盤面の評価には常に手番のプレイヤー視点で行うので、子盤面の評価値には-1を掛けて符号を逆転させることに注意してください。相手視点での最悪の評価値=自分視点での最良の評価値というわけです。


PVネットワークの実装

AlphaZeroのネットワーク構造はResNet-v1にpolicu headとvalue headが乗った構造となっています。せっかくなのでわりと論文に忠実に実装しましたが、オセロ程度なら正直もっとシンプルなネットワーク構造にしたほうが安定します。


学習結果

パフォーマンスの推移

GCPで 24-vCPU/64GB メモリ/NVIDIA Tesla P4 GPU のプリエンティブルVMインスタンスを使って4時間くらい学習した結果です*7。

横軸がselfplayの回数、縦軸がテスト用NPCと20回対戦した時の勝率となっています。

テスト用NPCは70%の確率で貪欲手（もっとも多くの石が取れる手）を選択し30%の確率でランダムな手を選択するアルゴリズムです。2000回のselfplayを終えたころにはほぼこのNPCには負けなくなっていることがわかります。

f:id:horomary:20210618191950p:plain:w400


人間 vs. AlphaZero

先手（黒）が人間で後手（白）がAlphaZeroです。普通に負けました。

f:id:horomary:20210619115017g:plain:w400
先手（黒）：人間, 後手（白）：Alpha Zero


次：MuZero

AlphaZeroの後継手法であるMuZero(2020)は、ボードゲームのように状態遷移が明らかな環境以外でも使える手法です。具体的にはAlphaZeroのアルゴリズムでブロック崩しができるようになりました。

horomary.hatenablog.com


参考

Deep Reinforcement Learning Hands-On

AlphaZero 深層学習・強化学習・探索 人工知能プログラミング実践入門

GitHub - PacktPublishing/Deep-Reinforcement-Learning-Hands-On: Hands-on Deep Reinforcement Learning, published by Packt

https://github.com/suragnair/alpha-zero-general

www.youtube.com


その他雑記

・Alpha Zeroの計算量について

対局時に本家AlphaZeroは一手につき800iterのPV-モンテカルロ木探索を行いますが、GPUによる推論は各iterでbatchsize=1の推論が一回なので、１手ごとにResNet-40相当のニューラルネットワークでの推論を800回行うことになります。

NVIDIAのベンチマークによると Jetson Nano （NVIDIAのGPU搭載ラズパイ的な製品）でも224×224の画像を１秒で38回推論（ResNet-50, FP16）できるらしいので、最近のGPUが１枚あれば人間との対戦では困らなさそうです。

推論ではなくトレーニングを高速化するためには、SelfPlayを可能な限り並列実行しつつその裏でネットワークを訓練し続けるApe-Xアーキテクチャが（たぶん）理想です。とくにSelfPlayの並列数が学習速度のボトルネックになるでしょうから、少数の高価なGPUを用意するよりは、並列selfplayのための安価なＧＰＵたくさん+勾配計算用の高性能GPU1枚 という構成がもっともコスパ良くトレーニングを高速化できると思います。

rayで実装する分散強化学習 ③Ape-X DQN - どこから見てもメンダコ


・これ強化学習？

AlphaZeroのニューラルネット更新は普通の教師あり学習でありQ学習ではありません。状態行動価値Qや方策ネットワークなど強化学習でおなじみの用語が登場しますが、ネットワーク更新方法としてのQ学習や方策勾配法は一切使われません。しかし、環境と相互作用してデータを自ら収集するという点においてはAlphaZeroは強化学習であると言えます。

AlphaZeroが強化学習かどうかという議論自体はどうでもいいのですが、モデルフリー強化学習の事前知識が無いと非常にconfusingです。


・モンテカルロ木探索という名称について

AlphaZeroのPV-MCTSではプレイアウト（ランダム対局）がニューラル盤面評価関数にとって代わられています。しかし、そもそもモンテカルロ木探索の ”モンテカルロ” はプレイアウト（ランダム対局）に由来するのでランダム対局をしないPV-MCTSが”モンテカルロ”であることには違和感があります。

これはUCTアルゴリズムのことを指して”モンテカルロ木探索”と言われることが多かったために、モンテカルロ要素であるプレイアウトが無くともわかりやすさのためモンテカルロ木探索と言っているのだと思います。（さすがにもう聞かないけど）携帯で写真をとることを”写メ”って言ってたようなものですね。


・ネットワークの改良について

AlphaZeroではネットワークにResNetを採用していますが、採用理由は開発当時にComputer Vision 分野での性能が良かったから程度で深い意味はないと思われます。CV向けのDLネットワークもここ数年でだいぶ進化しましたのでネットワーク構造を最先端のものに置き換えるだけでAlphaZeroのパフォーマンスが向上するかもしれません。

また、個人的に興味があるのは将棋分野でCNNをAttentionに置き換えることで性能が向上するのかどうかです。将棋では各ピクセル（マス目）にタテ・ヨコ・ナナメの情報を伝搬させることが囲碁よりも重要そうなので Axial attentionのような手法がうまくハマりそうな気がします。逆に囲碁はゲーム特性上CNNのままで問題なさそうな気もします。

[2003.07853] Axial-DeepLab: Stand-Alone Axial-Attention for Panoptic Segmentation


・オープニングブックについて

オープニングブックとは序盤の動きの定石を示すチェスの用語です。AlphaZeroのPV-MCTSでは過去のMCTSの履歴を近似する方策ネットワークを行動選択の事前分布（？）とするために、学習が進むにつれて特定のオープニングブックに収束していくと推測されます。

しかし、だからと言ってそれ以外のオープニングブックが明確に劣っているとは限らない、ということに注意してください。あくまでAlphaZeroの学習アルゴリズムがそのオープニングブックの深堀り研究（探索）を打ち切っただけです。たとえば、大器晩成型の複雑な戦術と先行逃げ切り型のわかりやすい戦術が同じ程度の強さだったとしても、AlphaZeroのアルゴリズムでは先行逃げ切り型に収束する確率が高い*8ことが予想されます。

よって、学習済みAlphaZeroに初動の制約をつけて追加訓練することにより、特定のオープニングブックに特化したAlphaZeroを作成することも可能なはずです。*9

Alのオープニングブックはついオラクル（神託）的に受け止めてしまいそうになりますが、少なくともAlphaZeroについては学習アルゴリズムをしっかり理解すれば「AIさんはそんな深く考えてないよ」という感じに思います。


*1:オセロで言えばカドをとられないようにするみたいな

*2:wiki（囲碁 - Wikipedia）によると囲碁のゲーム木複雑性は10400

*3:勝率は適当です。実際にシミュレーションしたわけではありません

*4:証明は割愛

*5:将棋なんかでは人間による盤面評価関数の設計がそれなりにうまくいっていたらしいです

*6:”モンテカルロ”の所以たるプレイアウトを排除したのにモンテカルロ木探索って呼称するのは混乱を招くと思う。ニューラルPUCTとかでいいんでは。

*7:メモリは16GBあれば十分だった

*8:探索と活用のトレードオフを決定するハイパラ調整次第ではあるけど

*9:このあたりのじゃんけん的な要素のがあるメタゲームをより深く研究したのがAlphaStarなのかもしれません