- はじめに
- DDPG (Deep Deterministic Policy Gradient) とは
- 学習を安定させるためのテクニック
- DDPGの問題点
- 実装
- 結果:Pendulum-v0
- 後継手法:TD3, SAC
- 備考: DDPGはoff-policy
はじめに
DDPG(決定論的方策勾配法, Deep Deterministic Policy Gradient)をtensorflow2で実装して連続値制御の基本タスクであるPendulum-v0を解きます。
※DDPGはDQNのエッセンスを多く含むため、DQNの理解が前提となります。
DPG (Deterministic Policy Gradient)): Deterministic Policy Gradient Algorithms
DDPG (Deep DPG): [1509.02971] Continuous control with deep reinforcement learning
DDPG (Deep Deterministic Policy Gradient) とは
一般的な方策勾配法では獲得報酬期待値が最大化されるように方策を最適化します。一方、DDPGではQ値が最大化されるように方策を最適化します。直感的には、Q関数を環境のシミュレータとして利用して方策を最適化していると見なすことができます。
また、DDPGでは方策関数が確率分布ではなくスカラ値を出力します。
一般的な方策勾配法で連続値制御を行う場合は、方策関数(Actor)はある状態の入力に対してアクションの確率分布を出力し、その確率分布からのサンプリングによってアクションを決めていました。典型的には状態Sを入力として正規分布パラメータ (μ, σ) を出力し、この平均μ、標準偏差σ の正規分布からアクションをサンプリングします。これは、方策勾配法に基づいて方策関数のパラメータを更新するためにはある状態sにおいてあるアクションa が選択される確率
が必要であるためです。(このような方策関数を確率的方策と呼称します。)
大雑把な説明ですが、方策勾配法とは における
の値が良好ならば
におけるの
の選択確率
が大きくなるように、逆なら小さくなるように更新するという手法です。ここで、もし方策関数がアクションの確率分布でなくスカラ値を出力するならば、
におけるの
の選択確率が計算できない(というか定義できない)ので方策勾配法が成立しません。
そのような方策勾配法の常識にも関わらず、DDPGの方策関数はある状態の入力に対してアクションが一意に決まるようなスカラ値を出力する関数なので決定論的方策と呼称されます。 決定論的方策では例えば状態sを入力としてスカラ値 a を出力します。
このような決定論的(スカラ値出力)方策 は、DPG論文が方策関数(Actor)のパラメータを、Q関数 (Critic) の出力値が大きくなるように更新するならば方策関数は確率分布が必須ではないよね、ということを示したことにより発見されました。冒頭にも書きましたが、直感的にはQ関数を環境のシミュレータとして利用して方策を最適化していると見なすことができます。

更新式内に、ある状態sにおいてあるアクションa が選択される確率 が式内に登場しないことに注意してください。
説明よりも実装を見た方が理解しやすいかもしれません。
DDPGのネットワーク構造
DQNスタイルのQ関数は入力が状態sのみでしたが、DDPGスタイルのQ関数(Critic)は状態sとアクションaの2つの入力を要求していることが上述の更新式からわかります。違いを図にしてみましょう。
左がDDPGスタイルのQ関数で右がDQNスタイルのQ関数です。

tensorflow2での実装はこんな感じ。
※2つの入力を必ずしも直接concatする必要はありません。隠れ層を噛ませて次元を揃えた後に和をとるみたいな実装も見かけました。
Q関数 (Critic) の更新
上式内の状態行動価値関数 Q の目的関数はDQNとほぼ同様です。
実装はこんな感じ
学習を安定させるためのテクニック
DDPGでは学習安定化のためのkey techniqueが2つ提案されています。
1. Soft-Target
DQNでは学習の安定化のためにTarget networkを導入しました。Target networkは定期的にMain Networkと重みを同期します。
このようなtarget networkの同期方法をhard targetと呼称します。hard targetでは”定期的に”を具体的に何ステップごとにするかが学習の安定性を大きく左右するハイパーパラメータとなってしまっているという問題があります。
そこで、論文ではMain NetworkをTarget networkが緩やかに後追いするsoft targetという手法を提案しています。τは更新率のハイパーパラメータであり論文では0.001を採用しています。
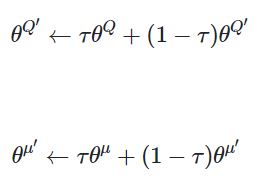
DQNではtargetの更新は10000stepごとに行っていましたが、DDPGではネットワークの更新頻度と同じくらい頻繁に少しずつ更新していきます。
この更新処理はtensorflow2.0では以下のように実装できます。
2. 探索ノイズ
DQNでは探索を促進するために、ε-Greedy(一定確率でランダム行動する)を採用していました。一方、DDPGでは探索を促進するために方策関数の出力であるアクションにノイズをのせます。論文ではOUノイズを採用していましたが、シンプルに平均ゼロのガウスノイズを乗せるだけでも問題なく機能するそうなのでこちらで実装しました。
Deep Deterministic Policy Gradient — Spinning Up documentation
DDPGの問題点
DQNに対するDouble DQN の指摘と同様に、DDPGは行動価値を過大評価することがTD3(Twin Delayed DDPG)論文で指摘されています。この問題は後継手法のTD3(Twin Delayed DDPG)では Double DQNと似たようなアプローチで解決することが提案されています。
また、決定論的方策ゆえにQ関数に似たような値ばかり渡すため、Q関数が過学習気味になり学習が不安定になりがちです。この問題はTD3ではQ関数の学習時には方策関数の出力したアクションにノイズを乗せることで解決を提案しています。
実装
コード全文はGithubを参照ください
結果:Pendulum-v0
Pendulum-v0では初期開始位置によって可能なスコアの上限が変わるのでこれくらいが実質的な限界パフォーマンスでしょう。

結果だけ見ると簡単そうですがハイパラ調整が地味に渋く、(MuJoCo向けに調整された)論文記載の学習率ではまったくスコアが上がりませんでした。
後継手法:TD3, SAC
備考: DDPGはoff-policy
DDPGはoff-policyです。off-policyなのでExperience Replayによる経験の使いまわしが可能なためサンプル効率が良いです。
しかし同じActor-CriticであるA2C/A3Cはon-policyです。なぜでしょう?
これはDDPGでは方策更新の指針となる を再評価できるが、A2C/A3Cでは方策更新の指針となるアドバンテージ
を再評価できないためです。
もっと具体的にはA3Cの方策更新の指針であるアドバンテージ関数内のは過去の方策による行動選択の結果であるため現在の方策更新の指針には使えないのでon-policyであるが、DDPGの方策更新の指針であるQ関数なら方策が更新されたら行動選択をやり直してQ関数の値を再評価すればいいのでオフポリシーというわけです。
言われてみればそりゃそうだという感じですが、私は当初混乱しました。